Légnedvesítéshez kapcsolódó
on-line, interaktív feladatgyűjtemény
Prof. Dr. Rajkó Róbert, Erdélyi Péter
Szegedi Tudományegyetem Mérnöki Kar, Folyamatmérnöki Intézet
2014
Tartalomjegyzék
1.2. A nedves levegő diagramjai
1.2.2. A pszichrometriai diagram
1.4. A pszichrometria élelmiszeripari alkalmazásai
2. Légnedvesítéshez kapcsolódó feladatok
2.1. Keresse meg az adott paraméterértékhez tartozó görbét!
2.2. Keresse meg a két megadott paraméterértékhez tartozó állapotpontot!
2.5. Keresse meg a megadott paraméterre melegített vagy hűtött levegő állapotpontját!
BEVEZETÉS
Az élelmiszer-feldolgozó és -tároló rendszerek tervezése és üzemeltetése, zöldség- és gyümölcsraktárak légkondicionálása, gabonafélék szárítása, hűtőtornyok méretezése stb. során a levegő jellemzőinek pontos ismerete elengedhetetlen. Sok élelmiszeripari nyersanyag, félkész vagy késztermék higroszkópos, azaz vizet vesz fel, vagy ad le a légtér hőmérsékletétől és relatív páratartalmától függő mértékben. A termodinamika, illetve a pszichrometria már tisztázta a levegő állapotváltozásával járó jelenségek elméleti alapjait, de a felmerülő problémák megoldására a gyakorlatban jól használható eszközökre van szükség. Az egyenletek papíron való megoldása, vagy a jelenleg rendelkezésre álló kézzel megszerkesztett, kisebb-nagyobb pontatlanságokat tartalmazó, többször fénymásolt, elmosódott diagramok használata nemcsak nehézkes, de leolvasási és interpolációs hibákkal is járhat. A modern számítástechnika eszközeivel ezek a problémák orvosolhatók.
Légnedvesítéshez kapcsolódó két kiemelt feladat: raktárak légkondicionálása, ill. meleg levegővel történő szárítás. Ezeknek a műveleteknek a végrehajtásához számításokat kell végezni, amelyeket legcélszerűbb interaktív feladatokon keresztül gyakoroltatni az alap, ill. mester képzések keretében.
A nedves levegő állapotjelzőinek kiszámítására alkalmas szoftver kifejlesztésével természetesen mások is foglalkoztak már. Harmatha (1987) algoritmust és működő programot kínál a probléma megoldására. A program képességei a számítások terén korlátozottak, grafikus megjelenítésre pedig nem ad útmutatást. A fentiek miatt határoztuk el egy, a légnedvesítéshez kapcsolódó feladatok megoldásához használható, a nedves levegő állapotjelzőinek megjelenítését célzó interaktív diagram kifejlesztését.
Az interaktív feladatok tartalomjegyzéke a http://hyde.fastmail.jp/toc.html címen található, valamint ebben a jegyzetben az elméleti ismeretek után feladatonként részletesebb megoldási útmutatót is adunk.
Ez a digitális tananyag a TÁMOP-4.1.1.C-12/1/KONV-2012-0004 pályázat támogatásával készült.
Jelölések
cp,a: a levegő fajlagos hőkapacitása, kJ/(kgK)
cp,j: a jég fajlagos hőkapacitása, kJ/(kgK)
cp,v: a víz fajlagos hőkapacitása, kJ/(kgK)
cp,vg: a vízgőz fajlagos hőkapacitása, kJ/(kgK)
h: fajlagos entalpia, kJ/kg
L0: a víz párolgáshője 0 °C-on, kJ/kg
Lh: a víz párolgáshője harmatponton (telítési hőmérsékleten), kJ/kg
pa: a levegő parciális nyomása, Pa
pv: a vízgőz parciális nyomása, Pa
pt: össznyomás (légköri nyomás), Pa
ps: telítési gőznyomás, Pa
rm: a víz és a levegő moláris tömegének hányadosa, rm= Mw / Ma = 0,62197
R: gázállandó, J/(mol K)
t: száraz hőmérő hőmérséklet, °C
td: harmatponti hőmérséklet, °C
tw: nedves hőmérő hőmérséklet, °C
T: hőmérséklet, K
V: térfogat, m3
y: nedvességtartalom, kg/kg
φ: relatív nedvességtartalom, %
ψ: telítési fok, %
1. Elméleti alapok
1.1. Pszichrometria
A pszichrometria a gőz-gáz elegyek termodinamikai tulajdonságainak meghatározásával foglalkozó tudományág. A kifejezés a görög ψυχρόν (hideg) és μέτρον (mérés) szavakból származik. Bár a pszichrometria elvei bármely gázból és gőzből álló fizikai rendszer leírására alkalmazhatók, a legelterjedtebben vizsgált elegy a levegő és a vízgőz keveréke, azaz a nedves levegő, ennek van ugyanis a legnagyobb gyakorlati jelentősége.
A száraz levegő több különböző gáz keveréke, összetétele a földrajzi hely és a tengerszint feletti magasság függvényében kissé változik. A két legnagyobb arányban jelenlévő komponens, az oxigén (O2) és a nitrogén (N2) aránya viszont közel állandó, a többi gáz mennyisége pedig elhanyagolható (1. táblázat).
Összetevő |
Térfogatszázalék |
|---|---|
Nitrogén (N2) |
78,084000 |
Oxigén (O2) |
20,947600 |
Argon (Ar) |
0,934000 |
Szén-dioxid (CO2) |
0,031400 |
Neon (Ne) |
0,001818 |
Hélium (He) |
0,000524 |
Egyéb gázok (metán (CH4), kén-dioxid (SO2), hidrogén (H2), stb.) |
0,000658 |
Összesen: |
100,000000 |
A környezeti levegő azonban sohasem teljesen száraz, mindig tartalmaz valamennyi vizet. A nedves levegő a száraz levegő és a vízgőz kétkomponensű elegyének tekinthető, melyben az előbbi gázként, jóval a kritikus hőmérséklete fölött, az utóbbi viszont gőzként, a kritikus hőmérséklete alatt van jelen, ezért könnyen kondenzálható. Mindkét összetevő tökéletes gáznak tekinthető, így az elegyük is, tehát alkalmazhatjuk rá az egyetemes gáztörvényt (Verhás, 1998).
Mikor a víz száraz levegővel érintkezik, párologni kezd, azaz gőzzé válik, és a gázfázisba vándorol. Ez a gőz azután nyomást fog kifejteni a folyadék felszínére, a parciális nyomást:
$${p}_{v}=\frac{R{\cdot}T}{{V}_{v}} .$$
Dalton törvénye szerint a nedves levegő össznyomása a száraz levegő és a vízgőz parciális nyomásának (résznyomásának) az összege:
$${p}_{t}={p}_{a}+{p}_{v} .$$
Az abszolút nedvességtartalom az egységnyi térfogatú nedves levegőben lévő víz tömege:
$$Y=\frac{{m}_{v}}{V}\left[\frac{kg}{{m}^{3}}\right] .$$
A gyakorlatban azonban célszerűbb a száraz levegő tömegét alapul venni, mert az az állapotváltozások során változatlan marad, ezért definiáljuk a fajlagos abszolút nedvességtartalmat (a továbbiakban röviden nedvességtartalom), mint 1 kg száraz levegőben lévő vízgőz tömegét:
$$y=\frac{{m}_{v}}{{m}_{a}}\left[\frac{kg}{kg}\right] .$$
Tehát y kg az a vízmennyiség, amely 1+y kg nedves levegőben van. Ez a mennyiség a moláris tömegek és a parciális nyomások hányadosával is kifejezhető:
$$y=\frac{{M}_{v}}{{M}_{a}}{\cdot}\frac{{p}_{v}}{{p}_{a}}=\frac{{M}_{v}}{{M}_{a}}{\cdot}\frac{{p}_{v}}{{p}_{t}-{p}_{v}}={r}_{m}{\cdot}\frac{{p}_{v}}{{p}_{t}-{p}_{v}} .$$
A levegő nedvességtartalma nem növekedhet minden határon túl. Amikor a gőz parciális nyomása elér egy bizonyos értéket, a telítési gőznyomást (ps), a levegőbe kerülő minden további vízmennyiség már csak folyadék formában (ködként) lehet jelen. A telítési gőznyomás a hőmérséklet nemlineáris függvénye, az összetartozó értékeket úgynevezett vízgőztáblázatból kereshetjük ki, illetve léteznek közelítő/interpolációs formulák, mint például az Antoine-egyenlet, amit később részletesen ismertetünk.
A telítési gőznyomáshoz tartozó összetétel a telítési nedvességtartalom, vagy telítési érték:
$${y}_{s}={r}_{m}{\cdot}\frac{{p}_{s}}{{p}_{t}-{p}_{s}} .$$
A relatív nedvességtartalom (vagy relatív páratartalom) a levegő telítethetőségének mértéke, azaz a víz keverékbeli parciális nyomásának és az azonos hőmérsékleten telített gőz nyomásának a hányadosa:
$$\varphi=\frac{{p}_{v}}{{p}_{s}} ,$$ vagy $$\varphi=100{\cdot}\frac{{p}_{v}}{{p}_{s}}\% .$$
Ha állandó pt össznyomáson (pl. nyílt rendszerben, légköri nyomáson) dolgozunk, akkor a vízgőz parciális nyomása sem lehet ennél nagyobb, még akkor sem, ha az adott hőmérsékleten a telítési gőznyomás értéke nagyobb az össznyomásnál (pl.: 130°C-on 3 bar), ezért ki kell egészítenünk a fenti definíciót:
$$\varphi=\frac{{p}_{v}}{{p}_{s}}\text{, ha }{p}_{s}{<}{p}_{t} $$ $$\varphi=\frac{{p}_{v}}{{p}_{t}}\text{, ha }{p}_{s}{\geq}{p}_{t} .$$
A telítési fok (vagy relatív telítettség) az előbbivel analóg fogalom, de a parciális nyomások helyett az összetételek hányadosával fejezi ki a telítethetőséget:
$$\psi=\frac{y}{{y}_{s}} .$$
A két mennyiség közötti kapcsolat:
$$\varphi=\psi{\cdot}\frac{{r}_{m}+{y}_{s}}{{r}_{m}+y} .$$
Minden anyagnak van valamekkora U belső energiája az őt alkotó elemi részecskék mozgásából és helyzetéből eredően. Ennek abszolút értéke nem határozható meg, de adott hőmérsékleten egy önkényesen megválasztott alapponthoz viszonyíthatjuk (Mujumdar, 2006). Ha egy állandó térfogatú nyugvó rendszer egy nála kisebb vagy nagyobb p nyomású környezettel kerül kölcsönhatásba, akkor V térfogatváltozást fog szenvedni, a térfogati munka: W=pV. E két mennyiség összege az entalpia:
$$H=U+p{\cdot}V\left[kJ\right] .$$
Az entalpia extenzív mennyiség. Ez azt jelenti, hogy – homogén rendszer esetén – értéke a rendszer méretével arányos. Célszerű bevezetni a fajlagos entalpia fogalmát, a tömegegységre vonatkoztatott entalpiát, amely viszont már kiterjedésétől függetlenül jellemzi a rendszert:
$$h=\frac{H}{m}\left[\frac{kJ}{kg}\right] .$$
A továbbiakban az entalpia szót kizárólag ebben az értelemben fogjuk használni.
A belső energiához hasonlóan az entalpia abszolút értéke sem határozható meg, de egy alkalmasan megválasztott referenciaállapothoz viszonyított relatív értéke igen. A víz entalpiáját nullának tekintjük folyadék halmazállapotban 0 °C-on és légköri (1 atm = 101325 Pa) nyomáson.
A fajlagos hőkapacitás, vagy fajhő az a hőmennyiség, amely egységnyi tömegű anyag hőmérsékletét egységnyivel növeli:
$${c}_{p}=\frac{Q}{m{\cdot}{\Delta}T}\left[\frac{kJ}{{kg}{\cdot}K}\right] .$$
Állandó nyomáson ez az energia egyenlő a belső energia és a nyomással szemben végzett munka összegével, vagyis az entalpiával, így
$${c}_{p}=\frac{h}{{\Delta}T} .$$
A tiszta anyag entalpiája:
$${h}={c}_{p}{\cdot}{\Delta}t ,$$
ahol Δt az alap (nulla) entalpiaállapot és az anyag hőmérsékletének különbsége.
Dalton törvényét felhasználva az y nedvességtartalmú levegő fajhője:
$$\left(1+y\right){\cdot}c=1{\cdot}{c}_{p,a}+y{\cdot}{c}_{p,vg} ,$$
azaz (1+y) kg tömegű nedves levegő fajhője egyenlő a komponensek tömegrészeinek és fajhőinek szorzatösszegével.
A száraz levegő entalpiája:
$${h}_{a}={c}_{p,a}{\cdot}t ,$$
a gőzé a párolgáshő és a túlhevítési hő összege:
$${h}_{v}={L}_{0}+{c}_{p,vg}{\cdot}t .$$
Az (1+y) kg tömegű nedves levegő entalpiája tehát:
$$h={h}_{a}+y{\cdot}{h}_{v}={c}_{p,a}{\cdot}t+y{\cdot}\left({L}_{0}+{c}_{p,vg}{\cdot}t\right) .$$
Ha a levegő túltelített, vagyis az ys telítési nedvességtartalom mellett (y-ys) mennyiségű ködként kicsapódott nedvességet is tartalmaz, akkor annak az entalpiáját 0 °C felett a folyékony víz fajhőjével kell számolnunk:
$$h={c}_{p,a}{\cdot}t+{y}_{s}{\cdot}\left({L}_{0}+{c}_{p,vg}{\cdot}t\right)+\left(y-{y}_{s}\right){\cdot}{c}_{p,v}{\cdot}t ,$$
0 °C alatt pedig a jég fajhőjével, továbbá a λ olvadáshőt is figyelembe kell vennünk:
$$h={c}_{p,a}{\cdot}t+{y}_{s}{\cdot}\left({L}_{0}+{c}_{p,vg}{\cdot}t\right)+\left(y-{y}_{s}\right){\cdot}\left({c}_{j}{\cdot}t-\lambda\right) .$$
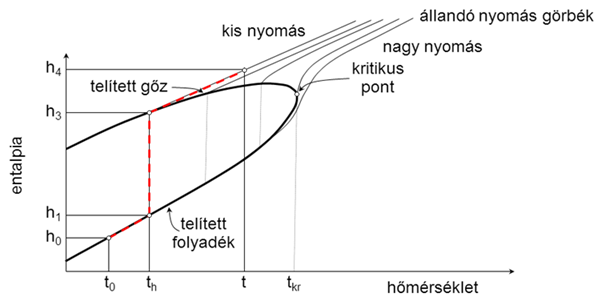
Az 1. ábrán bemutatott h–t diagramon azt láthatjuk, hogy valójában az állapotváltozás entalpia mérlege bonyolultabban számolható:
$$h={h}_{a}+y{\cdot}{h}_{v}={c}_{p,a}{\cdot}t+y{\cdot}\left({c}_{p,v}{\cdot}{t}_{h}+{L}_{h}+{c}_{p,vg}{\cdot}(t-{t}_{h})\right) .$$
A korábbi levezetéshez az egyszerűsítési lehetőséget az adta, hogy a víz alapállapoti hőmérsékletén elvégzett párologtatás során kapott állapotponthoz tartozó izobár nagyon közel fut a telítési hőmérséklethez tartozó izobárhoz (2. ábra), ezt az elhanyagolást a gyakorlatban széleskörűen elfogadják, bár jelen munka során a valódi állapotváltozáshoz (1. ábra) tartozó pontosabb képlete(ke)t alkalmaztuk.
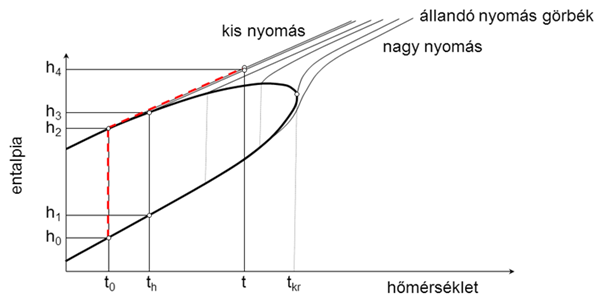
Az adiabatikus telítési hőmérséklet, vagy hűlési határhőmérséklet az a hőmérséklet, amelyet egy légtömeg akkor vesz fel, ha vizet párologtatva belé adiabatikusan (a környezetétől elszigetelve) hűtjük telítődésig úgy, hogy a látens hőt a légtömeg biztosítja. A belépő és a kilépő levegő entalpiája ilyenkor azonos, de az utóbbinak nagyobb a nedvességtartalma és alacsonyabb a hőmérséklete (Ibarz, 2003).
A levegő nedvességtartalmát pszichrométerrel (higrométerrel) mérhetjük meg. A legegyszerűbb az August-féle pszichrométer, ami két hőmérőből áll, melyek közül az egyik állandóan nedvesített gézbe van burkolva (nedves hőmérő). A másik, a száraz hőmérő a normál, hétköznapi értelemben vett léghőmérsékletet méri (száraz hőmérő hőmérséklet, a továbbiakban röviden hőmérséklet), a nedves hőmérő viszont mindig kevesebbet mutat (nedves hőmérő hőmérséklet), a felületéről elpárolgó víz hűti. A víz addig fog párologni, míg a hőmérő környezetében lévő levegő telítetté válik, a két hőmérő által mutatott érték különbsége pedig ezzel arányos lesz, ebből tehát következtethetünk a páratartalomra. Minél közelebb áll a levegő nedvességtartalma a telítésihez, annál kevesebb víz párolog el, ezért annál kisebb lesz az eltérés a száraz és a nedves hőmérő hőmérséklet között.
A nedves hőmérő hőmérséklet értéke vízgőz-levegő keverék esetén nagyon közel van az adiabatikus telítési hőmérséklethez, de nem azonos azzal. A víz párolgása látens hőt von el a nedvesített géztől (és a hőmérőtől), de ahogy az a száraz hőmérő hőmérséklet alá hűl, a levegőből szenzibilis hő áramlik felé, és növeli a hőmérsékletét. A folyamat végén beálló egyensúlyi hőmérséklet a nedves hőmérő hőmérséklet (Singh, 2009). Az Assmann-féle aspirációs pszichrométer abban különbözik az August-félétől, hogy a levegőt ventilátorral áramoltatja keresztül a készüléken. Ennek köszönhetően a nedves hőmérő hőmérséklet még inkább megközelíti a hűlési határhőmérsékletet (Fonyó, Fábry, 1998).
A harmatponti hőmérséklet az a hőmérséklet, melyre a levegőt le kell hűteni ahhoz, hogy telítetté váljon, miközben nedvességtartalma állandó marad. A harmatpont és a száraz hőmérő hőmérséklet közötti különbség szintén a nedvességtartalom függvénye. Minél kisebb a relatív páratartalom, annál nagyobb az eltérés. A harmatpont egyszerűen mérhető: egy fényes fémlapot annyira lehűtünk, hogy a felületére pára csapódik le a levegőből. Ezután várunk, míg melegszik, és a párafolt zsugorodik. Abban a pillanatban amikor eltűnik, leolvassuk a vele érintkeztetett hőmérőt (Bihari, 2001).
1.2. A nedves levegő diagramjai
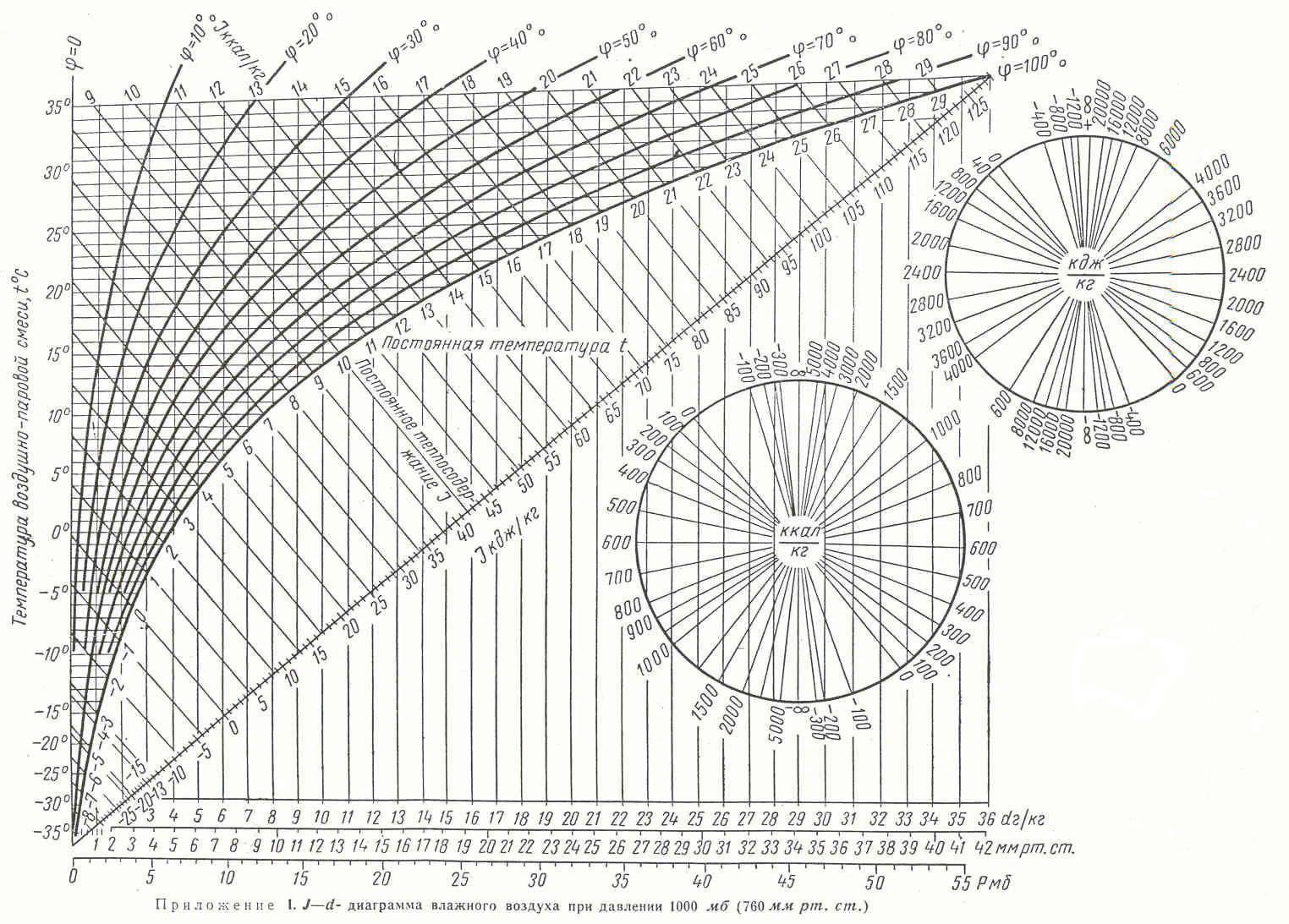
A fenti összefüggések alkalmazása légtechnikai műveletek tervezése során nehézkes, munkaigényes. Hatékonyabban elemezhetjük a folyamatokat, ha az állapotjelzőket diagramban szemléltetjük, és ezzel számítási műveleteket is megtakaríthatunk. A nedves levegő diagramjait három mérnök-tudós alkotta meg, egymástól függetlenül: az amerikai Willis Carrier 1911-ben, az orosz Leonid Konstantinovics Ramzin 1918-ban és a német Richard Mollier 1923-ban (Todorovic, 2007). Magyarországon, és általában Közép-Európában elsősorban a nedves levegő Mollier-féle h–y hőtartalom-diagramja használatos, az angolszász országokban pedig a Carrier-féle pszichrometriai diagram terjedt el. A Ramzin-diagram (3. ábra) a valamikori Szovjetunió területén volt népszerű (Todorovic, 2007), de mára kiszorult a használatból.
1.2.1. A Mollier-diagram
Ha a hagyományos módon, derékszögű koordináta-rendszerben ábrázoljuk az entalpiát a nedvességtartalom függvényében, akkor a gyakorlatban nehezen használható diagramot kapunk. Mint az 4. ábrán látható, a kék színű izotermák meredek szögben futnak felfelé, emiatt igen szűk a 100 % relatív páratartalom fölötti telítetlen mező, ami a szárítási folyamatok tervezése szempontjából a legfontosabb lenne (Beke, 1994). Azonban ha ferdeszögű koordináta-rendszert használunk, tehát a vízszintes tengelyt elforgatjuk lefelé, akkor a diagram hasznos területe jelentősen megnő. A Ramzin-diagram hasonló felépítésű, azzal a különbséggel, hogy egyszerűen 45°-os szöget használ (3. ábra). Mollier a h = ca ⋅ t + y ⋅ cv ⋅ t + y ⋅ L0 függvény a többihez képest nagy, a párolgáshővel arányos y ⋅ L0 tagját a vízszintes tengely alá mérte fel. Így az entalpiavonalak hajlásszöge kb. 50° (ez az aktuális diagramon alkalmazott léptékek függvényében változik), a 0 °C -os izoterma pedig pontosan vízszintes (Fonyó, Fábry, 1998). A 4. és 5. ábrákon az A és B pont távolsága y ⋅ L0 , a B–C távolság pedig ca ⋅ t + y ⋅ cv ⋅ t .
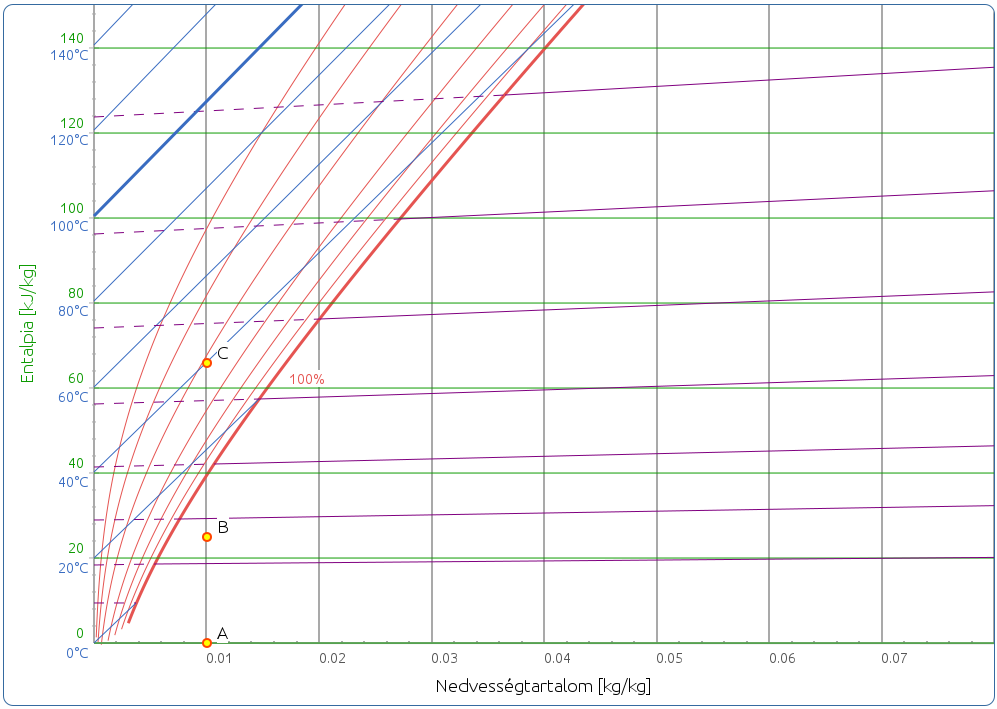
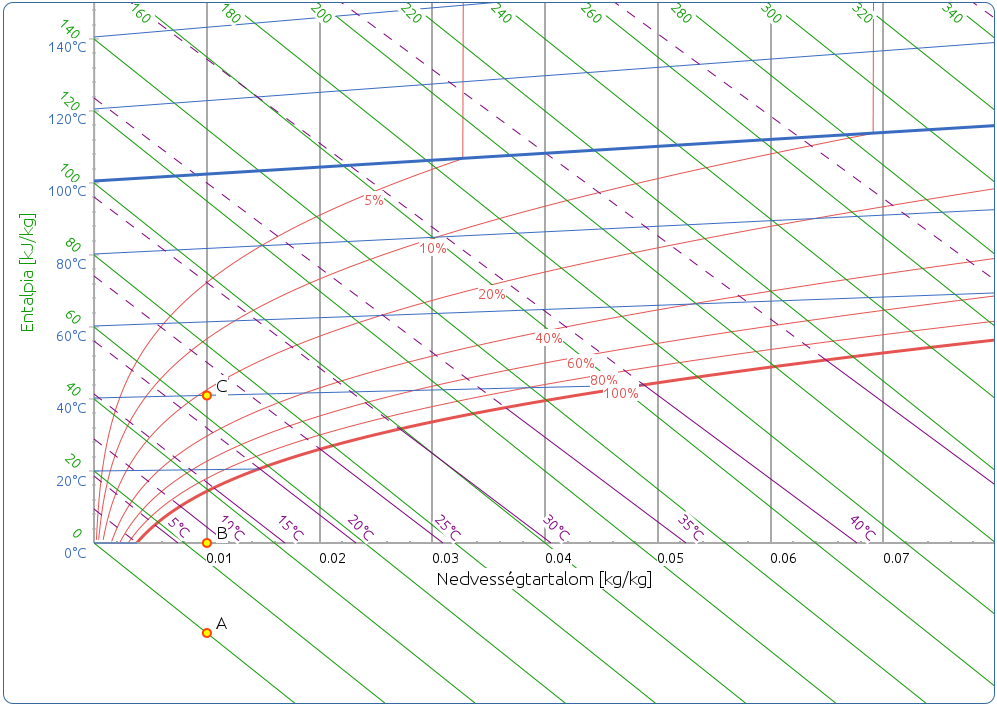
Az izotermákról fontos még megjegyezni, hogy a látszattal ellentétben nem párhuzamosak, hanem legyezőszerűen szétterülnek, meredekségük a hőmérséklet emelkedésével növekszik. A 100 %-os relatív páratartalom görbénél azonban megtörnek, és közel párhuzamossá válnak az entalpiavonalakkal, ott ugyanis a nedvességtartalom növekedésével az entalpia már csak a folyadékhővel növekszik. A telítési görbe alatti területet ködmezőnek, a töréspont utáni szakaszokat pedig ködizotermának nevezzük. Szokás a ködizotermákat meghosszabbítva a gőzmezőben is ábrázolni (szaggatott vonalak), hogy ezzel megkönnyítsük a nedves hőmérő hőmérséklet leolvasását, illetve a nedvességtartalom pszichrométerrel történő meghatározását (6. ábra).
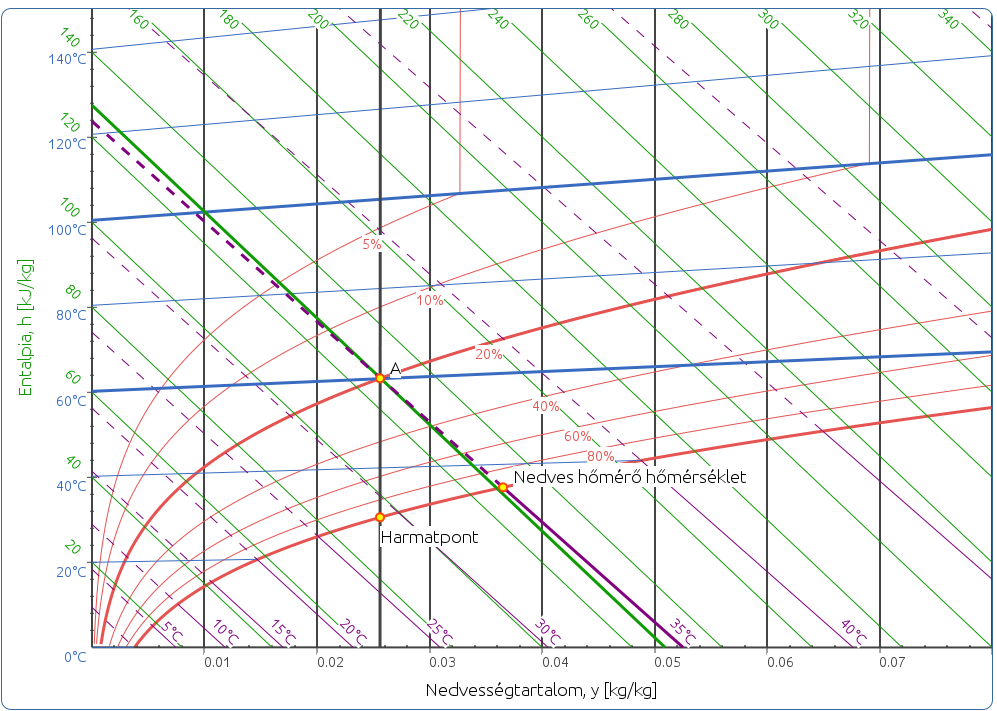
A relatív nedvességtartalom görbék a forrásponti izotermánál megtörnek, és függőlegesen felfelé futnak. A forráspont alatt φ a telítési gőznyomás, és ennélfogva hőmérséklet függvénye is. Definíció szerint a forráspont az a hőmérséklet, aminél a telítési gőznyomás eléri az össznyomást, ezt az értéket pedig nem haladhatja meg, tehát már nem függvénye a hőmérsékletnek, kizárólag az összetételnek.
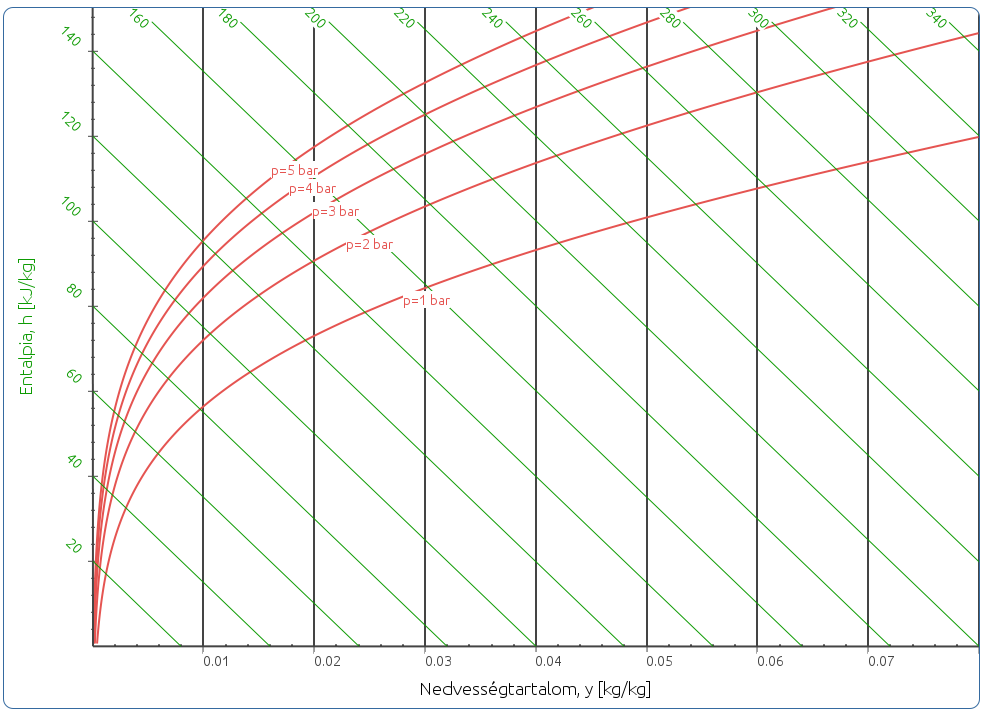
A diagram egy meghatározott össznyomásra készül (pl. 1 atm), egy izobár síknak tekinthető. Magasabb össznyomáson a relatív nedvességtartalom görbék felfelé tolódnak (7. ábra).
1.2.2. A pszichrometriai diagram
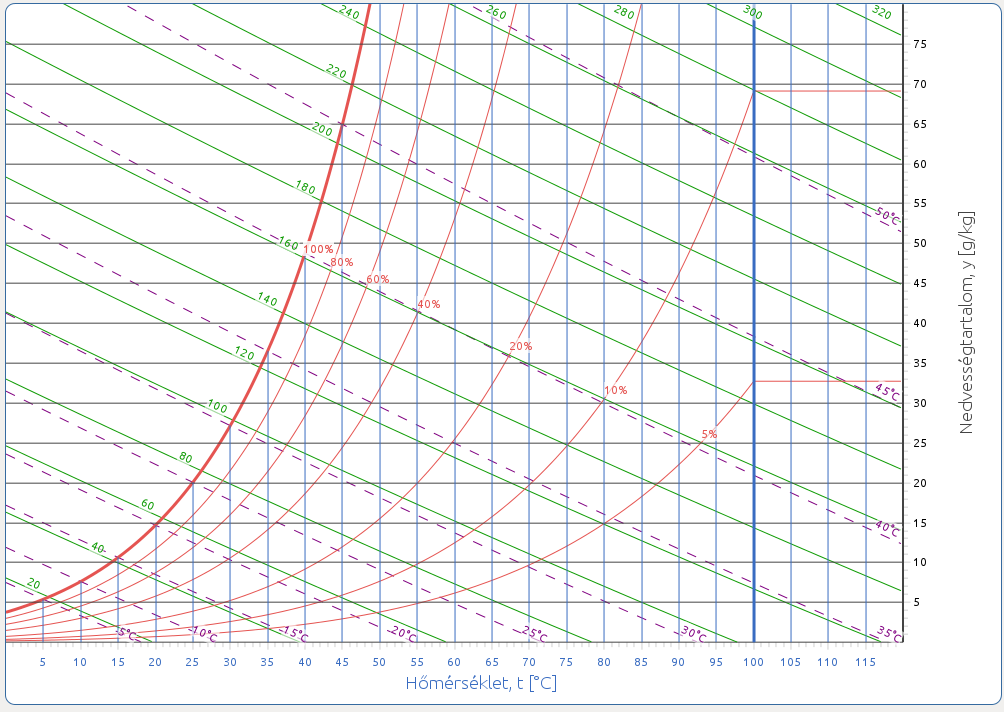
A Carrier-féle pszichrometriai (t-y) diagram (8. ábra) ugyanazokat a paramétereket tartalmazza, mint a Mollier-diagram, csak másképp ábrázolja. Tükrözéssel és 90°-os elforgatással az egyik diagram a másikba majdnem pontosan átvihető, de nem tökéletesen. Például míg a h-y diagramon az izotermák legyezőszerűen szétterülnek és távolságuk változik, a t-y diagramon egymástól egyenlő távolságban futó párhuzamos egyenesek. A kettő tehát teljesen egyenértékűen használható, pusztán történeti okokból preferálják a világ egyes részein az egyiket máshol a másikat.
Az egyes állapotjelzők meghatározása a pszichrometriai diagramon:
Száraz hőmérő hőmérséklet: az állapotpontból a kék színű, függőleges egyenesek (izotermák) mentén a vízszintes tengelyről olvasható le.
Nedves hőmérő hőmérséklet: a ködizotermák, vagy adiabaták (lila, ferde szaggatott vonalak) mentén.
Relatív páratartalom: hiperbolikus görbék, melyek a növekvő páratartalommal egyre közelebb kerülnek egymáshoz. A tökéletesen száraz levegő 0%-os görbéje a vízszintes tengelyen fekszik. A száraz és nedves hőmérő hőmérséklet vonalak a 100%-os relatív páratartalom görbénél, azaz a telítési görbénél találkoznak.
Harmatponti hőmérséklet: az állapotponthoz tartozó állandó nedvességtartalom vízszintes vonala és telítési görbe metszéspontja adja a harmatpontot. Az ehhez tartozó hőmérsékletet a fent említett módon olvashatjuk le.
Abszolút nedvességtartalom: a diagram vízszintes egyenesei mentén az ordinátán, vagyis a függőleges tengelyen határozható meg, mértékegysége: (g nedvesség) / (kg száraz levegő).
Fajlagos entalpia: az adiabatákkal közel párhuzamosan futó zöld vonalak mentén olvasható le.
1.3. Számítások
A számítások során gyakran szükséges a hőmérséklet és telítési gőznyomás közötti függvénykapcsolat használata, ennek pontos alakja azonban nem ismert. Az összetartozó hőmérséklet- és nyomásértékeket úgynevezett vízgőztáblázatokból kereshetjük ki. Hosszú adatsorokat begépelni azonban nem elegáns megoldás, kényelmetlen és hibákhoz is vezethet, ezért érdemes az Antoine-egyenletet használni, ami egyben interpolációt is végez az adatpontok között.
Az Antoine-egyenlet a telítési hőmérséklet és telítési gőznyomás összefüggését leíró interpolációs formula:
$$\ln\left({p}_{s}\right)=A+\frac{B}{C+{t}_{s}} ,$$
ahol A, B és C konstansok. A függvény egyszerűsége miatt nem elég rugalmas ahhoz, hogy a teljes telítési gőznyomás görbét pontosan leírja, ezért 50–60 °C-os intervallumonként más-más paraméterkészletet kell használni. A paramétereket meghatározhatjuk az adott hőmérséklet-tartomány három, vízgőztáblázatból vett hőmérséklet–nyomás értékpárjának segítségével (Harmatha, 1987). Ezeket az Antoine-egyenletbe helyettesítve egy háromismeretlenes egyenletrendszert kapunk, amely lineáris algebrai módszerekkel (Cramer-szabály) egyszerűen megoldható:
$$\begin{matrix}A{\cdot}C+A{\cdot}{t}_{s1}+B-C{\cdot}\ln\left({p}_{s1}\right)={t}_{s1}{\cdot}\ln\left({p}_{s1}\right)\\ A{\cdot}C+A{\cdot}{t}_{s2}+B-C{\cdot}\ln\left({p}_{s2}\right)={t}_{s2}{\cdot}\ln\left({p}_{s2}\right)\\ A{\cdot}C+A{\cdot}{t}_{s3}+B-C{\cdot}\ln\left({p}_{s3}\right)={t}_{s3}{\cdot}\ln\left({p}_{s3}\right) \end{matrix} $$
Az A, B, C konstansok 2. táblázatban található értékei a teljes telítési gőznyomás görbét hármasponttól a kritikus pontig lefedő, kb. 50 °C-os intervallumokban használhatók. A hőmérséklet és nyomás adatokat Fonyó, Fábry (1998) szakkönyvből vettük át.
pmin(Pa) |
pmax(Pa) |
tmin (°C) |
tmax (°C) |
A |
B |
C |
|---|---|---|---|---|---|---|
611,29 |
12000 |
0,00 |
49,45 |
23,7520 |
-4134,9088 |
238,5104 |
12000 |
100000 |
49,45 |
99,64 |
23,2125 |
-3827,3937 |
227,4984 |
100000 |
500000 |
99,64 |
151,48 |
24,2231 |
-4544,5633 |
257,9139 |
500000 |
1600000 |
151,48 |
201,36 |
24,5626 |
-5041,9476 |
289,2392 |
1600000 |
4000000 |
201,36 |
250,33 |
23,5217 |
-4106,8237 |
243,2856 |
4000000 |
8500000 |
250,33 |
299,24 |
24,0968 |
-4698,8506 |
277,9287 |
8500000 |
22120000 |
299,24 |
374,15 |
27,9045 |
-10287,6819 |
561,7324 |
A Gibbs-féle fázistörvény értelmében egy rendszer szabadsági fokainak (független állapotjelzőinek) száma: F = C – P + 2, ahol C a komponensek száma, P pedig a fázisok száma. A nedves levegő kétkomponensű, egyfázisú rendszer, ezért állapotát F = 2 – 1 + 2 = 3 változó egyértelműen meghatározza, tehát bármely három állapotjelző ismeretében az összes többi kiszámítható. Három változó ismerete nem csak elégséges, de szükséges feltétel is, háromnál több állapotjelző ugyanis már nem feltétlenül határoz meg egyértelműen egy állapotpontot.
Ha a fent ismertetett hét változóval számolunk (nyomás, száraz hőmérő hőmérséklet, nedves hőmérő hőmérséklet, harmatponti hőmérséklet, nedvességtartalom, relatív nedvességtartalom és entalpia), azok közül a nyomást kiemelve (feltételezve, hogy állandó nyomáson dolgozunk), a másik kettőt szabadon megválasztva a lehetséges esetek száma a hat változó másodosztályú, ismétlés nélküli kombinációinak számával egyenlő:
$${n \choose k}=\frac{6!}{2!{\cdot}4!}=15 .$$
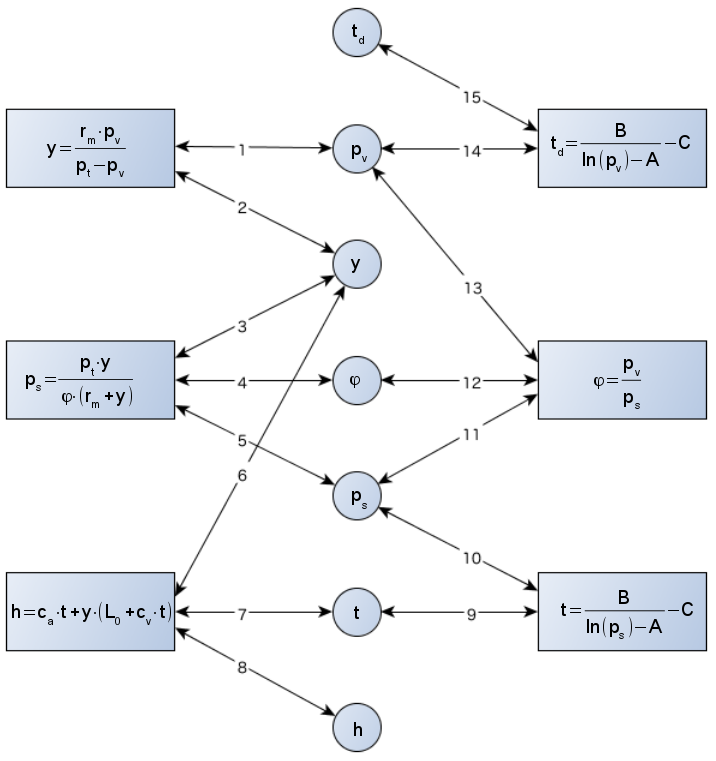
A t hőmérséklet, td harmatponti hőmérséklet, h entalpia, y nedvességtartalom, φ relatív nedvességtartalom, pv parciális gőznyomás és ps telítési gőznyomás közötti összefüggéseket a 9. ábra mutatja. Az egyenletekben szereplő többi tag konstans, vagy ismert változó (pt össznyomás). Az egyes esetekben használható algoritmusokat a 3. táblázat foglalja össze, a két ismert adatnak megfelelő sor, illetve oszlop cellájában lévő műveleteket kell elvégeznünk. Vegyük például a táblázat első celláját! Ismert t és h, ezekből a 9. ábrán a 8,7 → 6 utat követve kiszámíthatjuk y-t, valamint t-ből ps-t a 9-es úton. ps-ből és y-ból φ-t (5,3 → 4), y-ból pv-t (2 → 1), és végül td-t (→ 14).
| h |
y |
φ |
td |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| t |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| h |
|
? |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y |
|
X |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| φ |
|
A táblázatban „X”-szel jelöltük az állapotjelzők egyetlen párosát amiből nem lehet az állapotpontot meghatározni (harmatponti hőmérséklet és nedvességtartalom), a harmatpont ugyanis kizárólag a nedvességtartalom függvénye. Pozícióját a Mollier-diagramban egyértelműen meghatározza az adott pont y összetétele: az y-on átmenő függőleges egyenes és a φ=1 görbe metszéspontja. A tényleges állapotpontról csak annyi tudható, hogy az is erre az egyenesre esik, valahol a harmatpont fölött.
Egy kérdőjeles eset is van a táblázatban, ugyanis ha csak h és φ ismert, nincs egyszerű megoldás a 9. ábra összefüggéseinek felhasználásával. Az entalpia csak a
$$h={c}_{a}{\cdot}t+y{\cdot}\left({L}_{0}+{c}_{v}{\cdot}t\right)$$
kifejezésben szerepel, de a t hőmérséklet és az y nedvességtartalom is ismeretlen. y-t ki tudjuk fejezni φ-vel. Definíció szerint:
$$y={r}_{m}{\cdot}\frac{{p}_{v}}{{p}_{t}-{p}_{v}}$$ és $${p}_{v}=\varphi{\cdot}{p}_{s} ,$$
ezekből
$$y=\frac{{r}_{m}{\cdot}\varphi{\cdot}{p}_{s}}{{p}_{t}-\varphi{\cdot}{p}_{s}} .$$
A pstelítési gőznyomás szintén ismeretlen, viszont az Antoine-egyenlet révén a hőmérsékletet is ki tudjuk vele fejezni, és akkor az egyenlet egyismeretlenessé válik. Ezeket behelyettesítve:
$$h=\frac{{c}_{a}{\cdot}B}{\ln\left({p}_{s}\right)-A}-C+\frac{{r}_{m}{\cdot}\varphi{\cdot}{p}_{s}}{{p}_{t}-\varphi{\cdot}{p}_{s}}{\cdot}\left({L}_{0}+\frac{{c}_{v}{\cdot}B}{\ln\left({p}_{s}\right)-A}-C\right) .$$
Az egyenlet komplikáltnak tűnik, de átalakítás, a konstansok összevonása után egyszerűbb formában is felírható:
$$\ln\left({p}_{s}\right)=c{\cdot}{p}_{s} .$$
Ha ebből kiszámítanánk ps-t, akkor t-t és y-t is megkapnánk. Csakhogy ezt az egyszerű egyenletet nem lehet analitikusan megoldani, ugyanis ps lineáris és logaritmikus alakban is szerepel benne. Az exponenciális függvény alkalmazásával ki tudjuk hozni a logaritmusból:
$${p}_{s}=c'{\cdot}{e}^{{p}_{s}} ,$$
így viszont az eddig lineáris tag kitevőbe kerül, ahonnan csak logaritmálással tudjuk kihozni, amivel visszajutunk az eredeti problémához. Analitikus megoldás híján közelítő megoldást kell találnunk.
A szelőmódszer a numerikus analízis évezredek óta ismert eszköze függvények gyökének közelítésére. (Papakonstantinou, 2007). Hasonló a Newton-módszerhez, de azzal ellentétben alkalmazása nem kívánja meg a függvény deriváltjának ismeretét.
Az eljárás lényege a következő: két becsült értékből (x0 és x1) kiindulva kiszámítjuk az f(x0) és f(x1) függvényértékeket. Ezek egy-egy pontot határoznak meg a függvény gráfján, amelyeket összekötő egyenes egyenlete:
$$y=\frac{f\left({x}_{1}\right)-f\left({x}_{0}\right)}{{x}_{1}-{x}_{0}}{\cdot}\left({x}_{2}-{x}_{0}\right)+f\left({x}_{1}\right) .$$
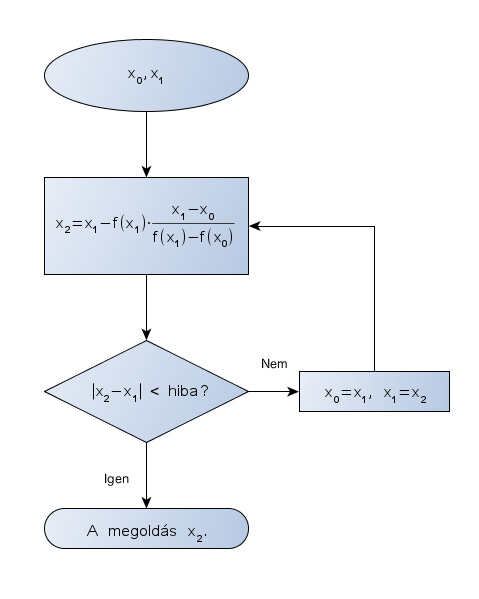
Ha megkeressük az egyenlet gyökét, vagyis y=0-t behelyettesítve megoldjuk az egyenletet x2-re, az alábbi összefüggéshez jutunk:
$${x}_{2}={x}_{1}-f\left({x}_{1}\right){\cdot}\frac{{x}_{1}-{x}_{0}}{f\left({x}_{1}\right)-f\left({x}_{0}\right)} .$$
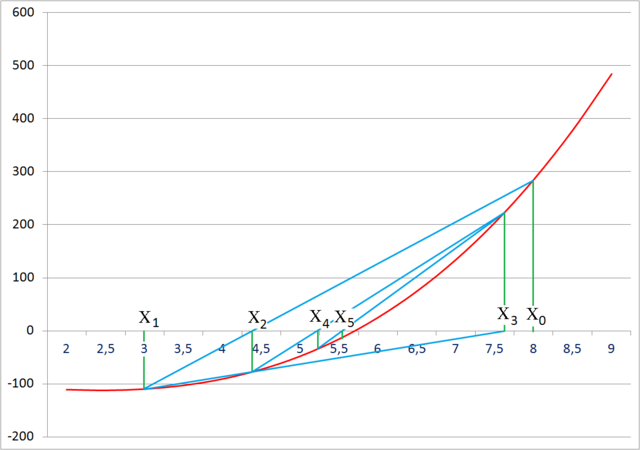
Ezután a kapott x2 értéket x1-nek, x1-et x0-nak véve újra kiértékeljük a fenti egyenletet. Ezt az eljárást addig ismételjük, míg két egymást követő gyök közötti különbség elegendően kicsi nem lesz. A folyamatot a 10. ábra szemlélteti. Mint a 11. ábrán látható, a konvergencia viszonylag gyors (bár meg kell jegyeznünk, hogy nem mindig konvergál, de ez szerencsére nem az az eset).
A ps-re adott két becslés legyen 0 és az össznyomás, ugyanis ezek a függvény értelmezési tartományának a végpontjai, a keresett érték mindenképp ezen határok közé esik. 0 és 105 Pa között a hiba mindössze öt iterációs lépés után 1 Pa alá csökken.
Példaként a nedves hőmérő hőmérséklettel kapcsolatos számításokat részletesebben is bemutatjuk.
Ha adott a hőmérséklet és a nedves hőmérő hőmérséklet
A telített levegő entalpiája és nedvességtartalma egyszerűen meghatározható:
$${h}_{s}={c}_{a}{\cdot}{t}_{w}+{y}_{s}{\cdot}\left({L}_{0}+{c}_{v}{\cdot}{t}_{w}\right)$$
és
$${y}_{s}=\frac{{r}_{m}{\cdot}{p}_{s}}{{p}_{t}-{p}_{s}} .$$
Az entalpia a ködmezőben, a telítési görbe alatt, ahol (y-ys) mennyiségű kondenzálódott víz is van a levegőben:
$$h={h}_{s}+\left(y-{y}_{s}\right){\cdot}{c}_{w}{\cdot}{t}_{w} ,$$
ahol cw a víz fajhője. Ebben kifejezésben két ismeretlen szerepel, h és y, a megoldáshoz tehát szükségünk van még egy egyenletre. A keresett állapotpont entalpiája:
$$h={c}_{a}{\cdot}t+y{\cdot}\left({L}_{0}+{c}_{v}{\cdot}t\right) .$$
A keresett állapotpont az entalpiavonalának és a telítési pontján átmenő adiabatának a metszéspontja:
$${h}_{s}+\left(y-{y}_{s}\right){\cdot}{c}_{w}{\cdot}{t}_{w}={c}_{a}{\cdot}t+y{\cdot}\left({L}_{0}+{c}_{v}{\cdot}t\right) .$$
y-t kifejezve:
$$y=\frac{{h}_{s}-{c}_{a}{\cdot}t-{y}_{s}{\cdot}{c}_{w}{\cdot}{t}_{w}}{{L}_{0}+{c}_{v}{\cdot}t-{c}_{w}{\cdot}{t}_{w}} ,$$
majd visszahelyettesítve az entalpia egyenletébe h-t is megkapjuk. A többi állapotjelző meghatározása a korábban ismertetett módon lehetséges.
Ha adott a nedvességtartalom és a nedves hőmérő hőmérséklet
A nedves hőmérő hőmérsékletből kiszámítjuk a ps telítési gőznyomást. Mivel a telítési pontban φ=1,
$${y}_{s}=\frac{{r}_{m}{\cdot}\varphi{\cdot}{p}_{s}}{{p}_{t}-\varphi{\cdot}{p}_{s}}=\frac{{r}_{m}{\cdot}{p}_{s}}{{p}_{t}-{p}_{s}} .$$
Ebből számíthatjuk a hs telítési entalpiát, mint fent. Mivel y most ismert, az entalpiát meghatározhatjuk h = hs + (y - ys) ⋅ cw ⋅ tw-ből, majd a hőmérsékletet h = ca ⋅ t + y ⋅ (L0 ⋅ cv ⋅ t)-ből.
Ha adott az entalpia és a nedves hőmérő hőmérséklet
Ugyanazokat az összefüggéseket használhatjuk, mint az előző esetben.
Ha adott az relatív nedvességtartalom és a nedves hőmérő hőmérséklet
A már ismert módon kiszámítjuk ys-t és hs-t. A korábban részletesen ismertetett szelőmódszerrel hs-ből és φ-ből meghatározzuk a telítési gőznyomást, és ezt vesszük a h-hoz tartozó telítési gőznyomás első becslésének.
$y=\frac{{r}_{m}{\cdot}\varphi{\cdot}{p}_{s}}{{p}_{t}-\varphi{\cdot}{p}_{s}}$-ből számolva teszünk egy kezdeti becslést y-ra és $h={h}_{s}+\left(y-{y}_{s}\right){\cdot}{c}_{w}{\cdot}{t}_{w}$-ből h-ra. A kapott h-ból és φ-ből kiszámítunk egy újabb, pontosabb értéket ps-re, majd y-ra és h-ra. Ezt iteratívan folytatjuk, míg el nem érjük a kellő pontosságot. A tapasztalat szerint az eltérés már a harmadik iteráció után 1 % alá csökken.
Ha adott a harmatpont és a nedves hőmérő hőmérséklet
A td harmatpontból az Antoine-egyenlettel kiszámíthatjuk a pv parciális gőznyomást, ugyanis a harmatpont az a hőmérséklet, amin az adott összetételű elegy telített.
$y=\frac{{r}_{m}{\cdot}{p}_{v}}{{p}_{t}-{p}_{v}}$, innentől pedig y-ból úgy számolhatunk, mint fent.
A nedves hőmérő hőmérsékletet meghatározása
Ehhez szükséges h és y ismerete. Számítsuk ki a h-hoz és φ=1-hez tartozó ps telítési gőznyomást a szelőmódszerrel, majd az ehhez tartozó hőmérsékletet az Antoine-egyenlettel. Ez lesz az első becslésünk tw-re. tw-ből a már ismertetett eljárással kiszámítjuk ys-t, abból hs-t, végül a tényleges nedves hőmérő hőmérsékletet hs-ből és φ=1-ből.
1.4. A pszichrometria élelmiszeripari alkalmazásai
1.4.1. Klimatizálás
A légkondicionálás célja, hogy a levegőt különböző paramétereinek, elsősorban hőmérsékletének és páratartalmának megváltoztatása révén számunkra kedvezőbb állapotba hozzuk. Fontosabb alkalmazási területei az élelmiszeriparban:
Zöldség- és gyümölcsraktárak légterének szabályozása
A zöldségek, gyümölcsök légzése - bár lecsökkent mértékben - de betakarítás után is folytatódik. Ez a folyamat biológiailag szükséges, de hosszabb tárolás során a szén-dioxid és víz formájában eltávozó szénhidrátmennyiség tömegcsökkenést okoz (légzési veszteség). További problémákat okozhat a légzés hőtermelése is (Bara, 2008). A légzés során távozó pára lecsapódhat, ez pedig mikrobiológiai romláshoz vezethet. A légzésintenzitást a hőmérséklet és a nedvességtartalom szabályozásával optimális értéken tarthatjuk, megőrizve ezzel a termék minőségét és minimalizálva a légzési veszteséget. A friss gyümölcsöket alacsony hőmérsékletű, magas relatív páratartalmú légtérben tárolva lassíthatjuk azok anyagcsere-folyamatait.
Sajtok, húsipari termékek érlelése
Az érlelés során a levegő hőmérsékletét és páratartalmát a termék jellegének megfelelően kell beállítani és a folyamat során változtatni. A művelet célja gyakran egyben a szárításos tartósítás is, ilyenkor a levegő áramlási sebességét is szabályoznunk kell.
1.4.2. Szárítás
Szárításon általános értelemben olyan folyamatot értünk, melynek során illékony anyagok (nedvesség) eltávolításával szilárd terméket állítunk elő. A gyakorlatban leggyakrabban meleg levegős szárítást végzünk, melynek során a nedvesség (víztartalom) csökkentése vagy eltávolítása a cél, tehát a szárítás olyan művelet, amelynek során a szilárd anyag belsejéből a nedvesség diffúzióval jut a szilárd anyag felületére, onnan a szárító levegőbe és azzal együtt távozik. A folyamat hajtóereje az a gőznyomáskülönbség lesz, amely az adott hőmérsékletű nedves anyagban lévő víz gőznyomása és a szárító levegőben lévő vízgőz parciális nyomása között fennáll. A célunk lehet tartósítás és/vagy anyaghányad-csökkentés.
Konvekciós szárítás során előmelegített, a szárítandó anyag egyensúlyi relatív páratartalmánál (ERP) alacsonyabb páratartalmú levegőt áramoltatunk a szárítandó anyag mellett, ebbe párolog az anyag víztartalma, továbbá ez a levegő fedezi a nedvesség elpárologtatásnak és az anyag felmelegítésének hőszükségletét is.
Az érzékeny élelmiszeripari nyersanyagok kíméletes szárításának megvalósítása érdekében gondosan kell megválasztanunk a szárítólevegő paramétereit, továbbá energiagazdálkodási szempontokat is figyelembe kell vennünk (pl. a szárítóból kilépő levegő hőtartalmának újrahasznosítása a belépő levegőhöz való keveréssel).
2. Légnedvesítéshez kapcsolódó feladatok
Az interaktív feladatok tartalomjegyzéke a http://hyde.fastmail.jp/toc.html címen található, illetve az egyes feladatok a lenti linkekre kattintva közvetlenül is elérhetőek. A feladatok megoldása során, a kezdőképernyőn megjelenik a feladat szövege, valamint egy, a diagramon feltüntetett állapotpontok adatait tartalmazó táblázat. Ha a feladatot jól oldottuk meg, a táblázat kiegészül a többi paraméterrel. A "Megoldás" gombra kattintva, a program animáció segítségével bemutatja a megoldást. Az "Új feladat" gombra kattintva ugyanazt a feladatot újabb véletlenszerűen választott adatokkal gyakorolhatjuk. Az oldal tetején található linkekkel navigálhatunk a feladatok között előre-hátra, illetve vissza a tartalomjegyzékhez.
2.1. Keresse meg az adott paraméterértékhez tartozó görbét!
http://hyde.fastmail.jp/exercises.html#showex1
Kattintson az egérrel az adott izotermára, relatív páratartalom görbére, stb. Helyes válasz esetén a görbe vastagítva jelenik meg (12. ábra). Ebben a feladatban csak a diagramon már feltüntetett görbék szerepelnek kérdésként.
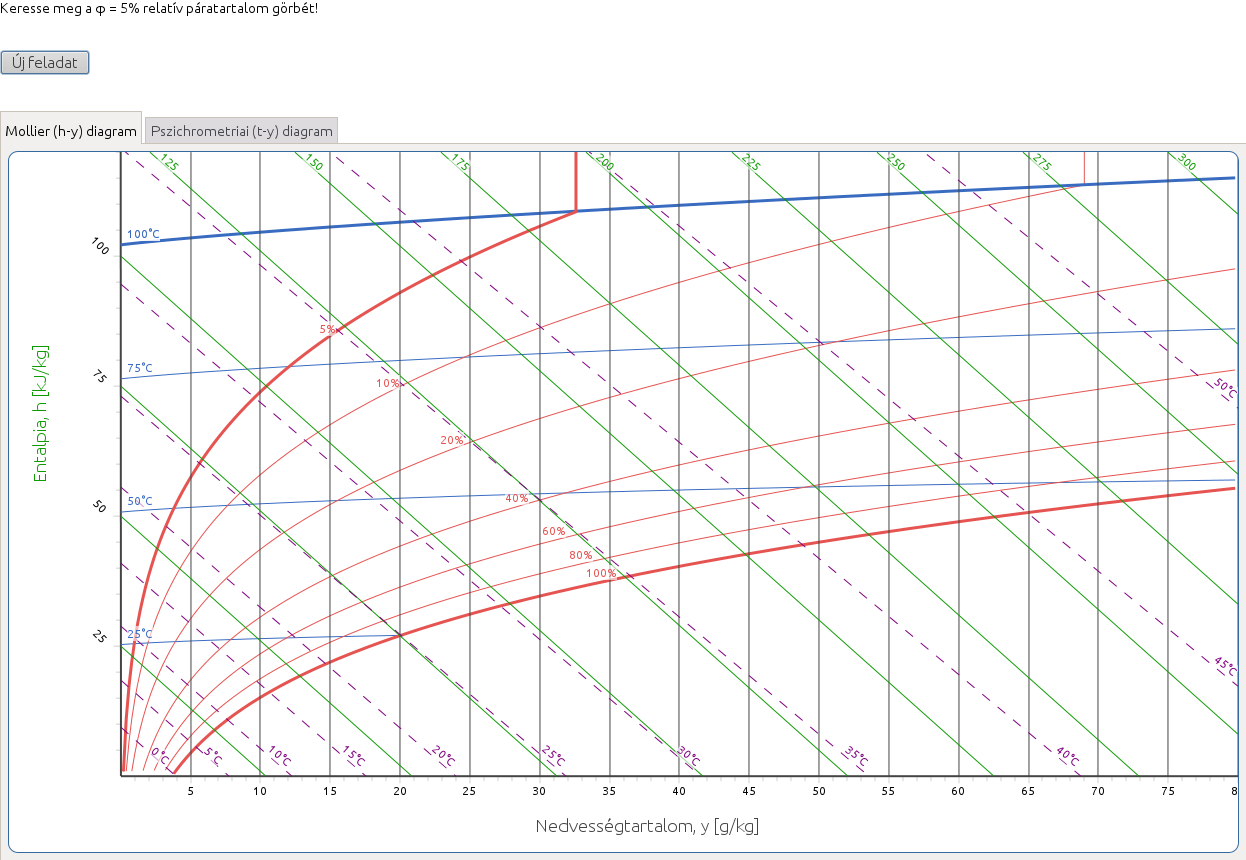
2.2. Keresse meg a két megadott paraméterértékhez tartozó állapotpontot!
http://hyde.fastmail.jp/exercises.html#showex2
Egy légtömeg állapotát (állandó nyomáson) bármely két független állapotjelzője egyértelműen meghatározza. A Mollier-féle h–y és a Carrier-féle pszichrometriai diagramokon az állapotjelzőkhöz tartozó görbék metszéspontja, az állapotpont mutatja a nedves levegő helyzetét. Az ebben a feladatban megadott paraméterek görbéi már nem feltétlenül szerepelnek a diagramon, ezért interpolálnunk kell. Figyeljük meg, hogy a relatív páratartalom görbék a telítési görbétől távolodva ritkulnak, tehát például a 13. ábrán látható esetben a 35%-os görbe jóval közelebb esik a 40%-os görbéhez, mint azt várnánk. Itt a másik megadott paraméter a harmatponti hőmérséklet volt. (A harmatpont megkereséséhez segítségül lásd 3. feladathoz tartozó megjegyzést.)
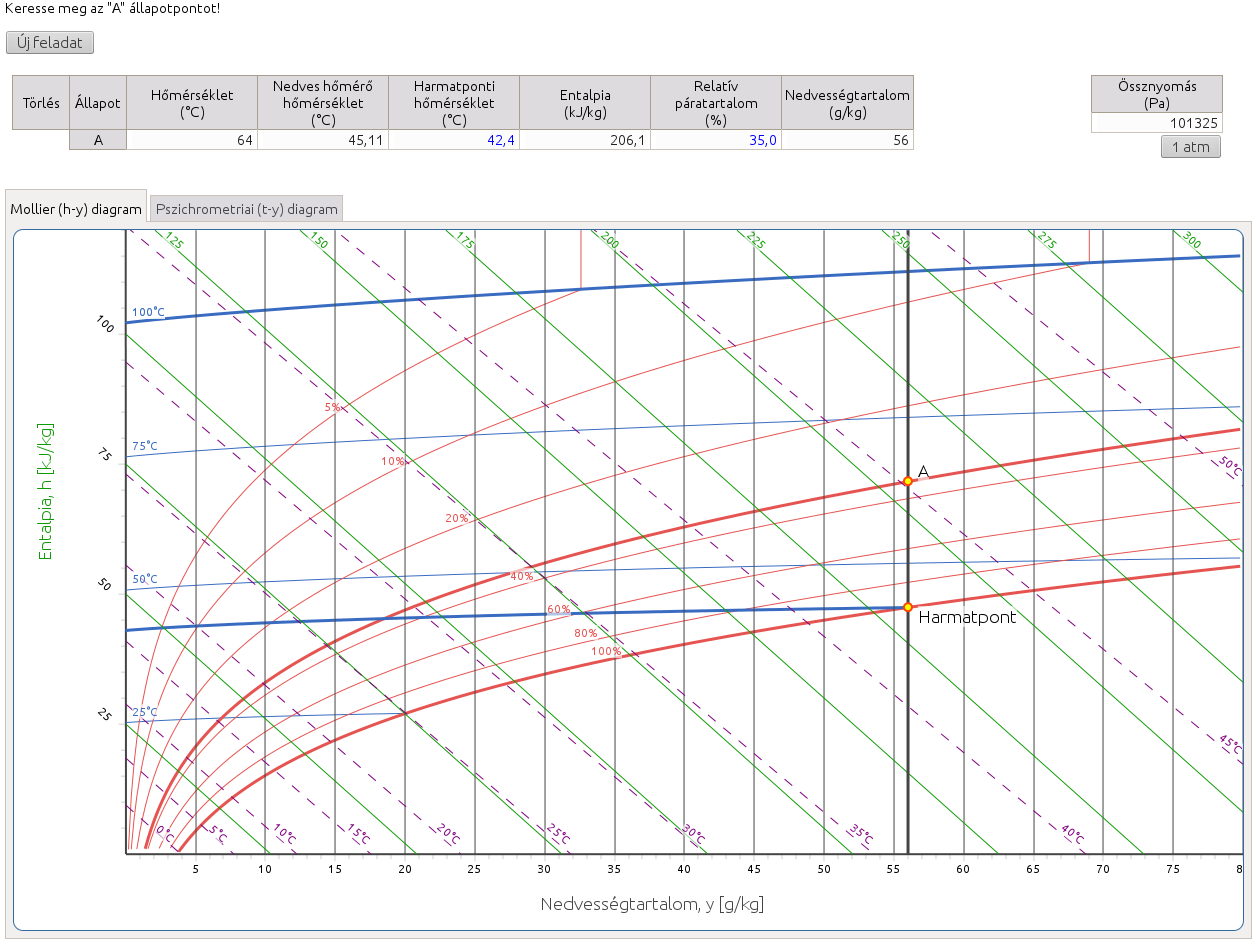
Mivel az adiabaták közel párhuzamosan futnak az entalpiavonalakkal és a metszéspontjukat nehéz megtalálni, ezért a paraméterek ezen párosítása nem szerepel feladatként, de természetesen ezzel a két adattal is lehetséges a légállapot meghatározása.
2.3. Keresse meg az adott állapotponthoz tartozó harmatpontot, és határozza meg a harmatponti hőmérsékletet!
http://hyde.fastmail.jp/exercises.html#showex3
A harmatponti hőmérséklet az a hőmérséklet, melyre a levegőt le kell hűteni ahhoz, hogy telítetté váljon, miközben nedvességtartalma állandó marad. Az állapotpontból tehát a Mollier-féle h–y diagramon függőlegesen lefelé, a Carrier-féle pszichrometriai diagramon vízszintesen balra kell haladnunk, amíg elérjük a telítési görbét, ezzel meghatározzuk a harmatpontot. Ezután a Mollier-féle h–y diagram függőleges tengelyéről, illetve a Carrier-féle pszichrometriai diagram vízszintes tengelyéről leolvassuk a hozzá tartozó hőmérsékletet.
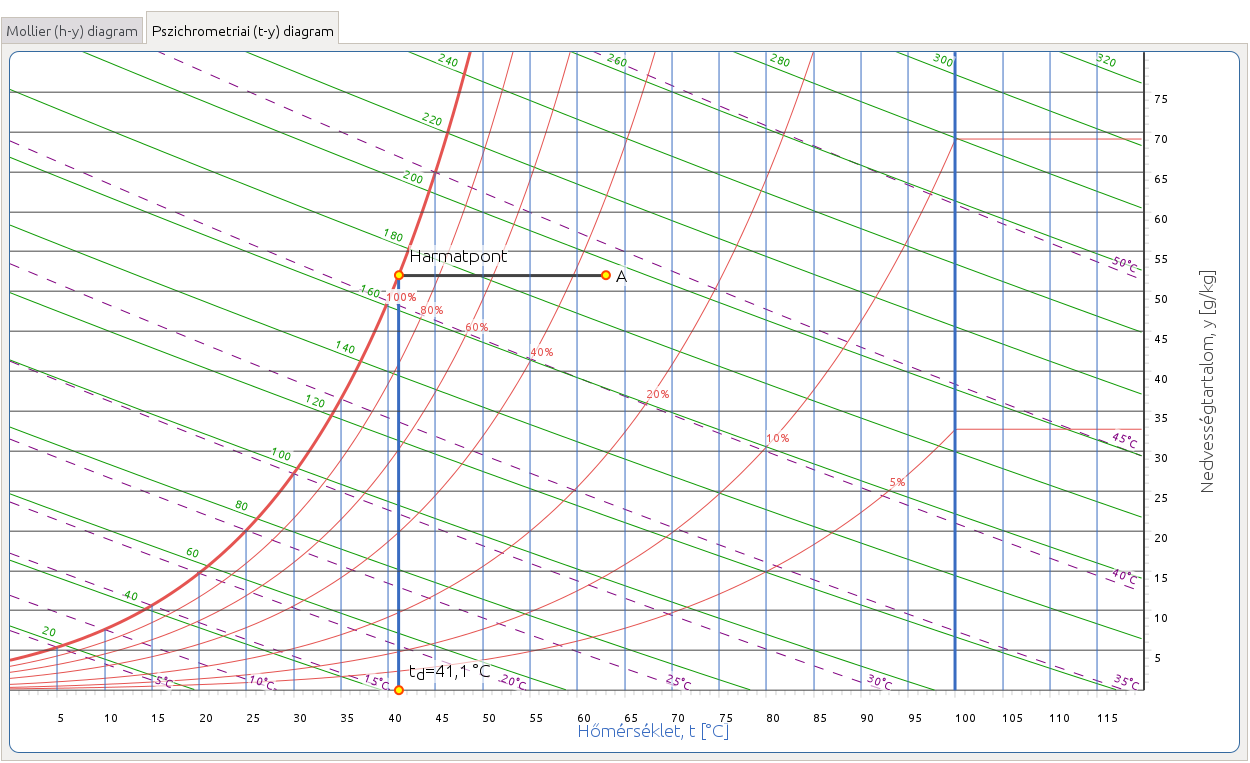
2.4. Keresse meg a ködmezőben lévő állapotponthoz tartozó harmatpontot, és a köd gázfázisának állapotpontját!
http://hyde.fastmail.jp/exercises.html#showex4
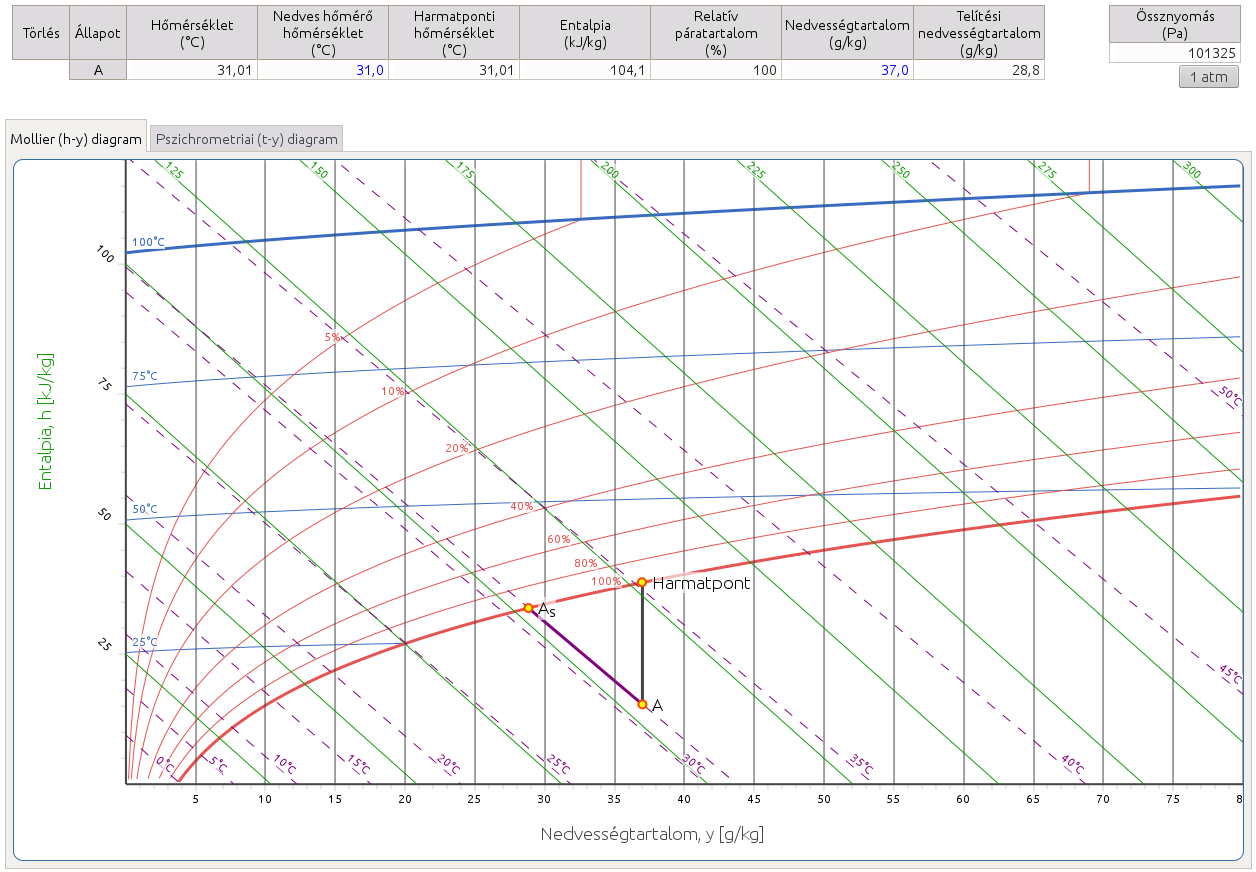
Ha a nedves levegőt a harmatponti hőmérséklete alá hűtjük, akkor átlépjük a telítési, azaz 100%-os relatív páratartalom görbét, a levegő túltelítetté válik, a gőz vízcseppek formájában kiválik és köd képződik. A Mollier-féle h–y diagramon a telítési görbe feletti területet gőzmezőnek, az az alattit ködmezőnek nevezzük. A Carrier-féle pszichrometriai diagramon a ködmező a bal felső sarokban helyezkedik el. Az "A" állapotpont tehát egy kétfázisú rendszert jelöl, amely telített levegőt és diszpergált állapotú folyékony vizet is tartalmaz. A harmatpont alá hűtés tehát egyben a nedvességtartalom csökkenését is eredményezi, ezért a gázfázis "As" állapotpontja a Mollier-diagramon az "A" ponttól balra, a pszichrometriai diagramon az alatt található, egészen pontosan az "A"-n áthaladó adiabata (ködizoterma, állandó nedves hőmérő hőmérséklet görbe) és a telítési görbe metszéspontja adja. A kikondenzálódott víz mennyisége az eredeti nedvességtartalom és a telítési nedvességtartalom különbségeként számítható.
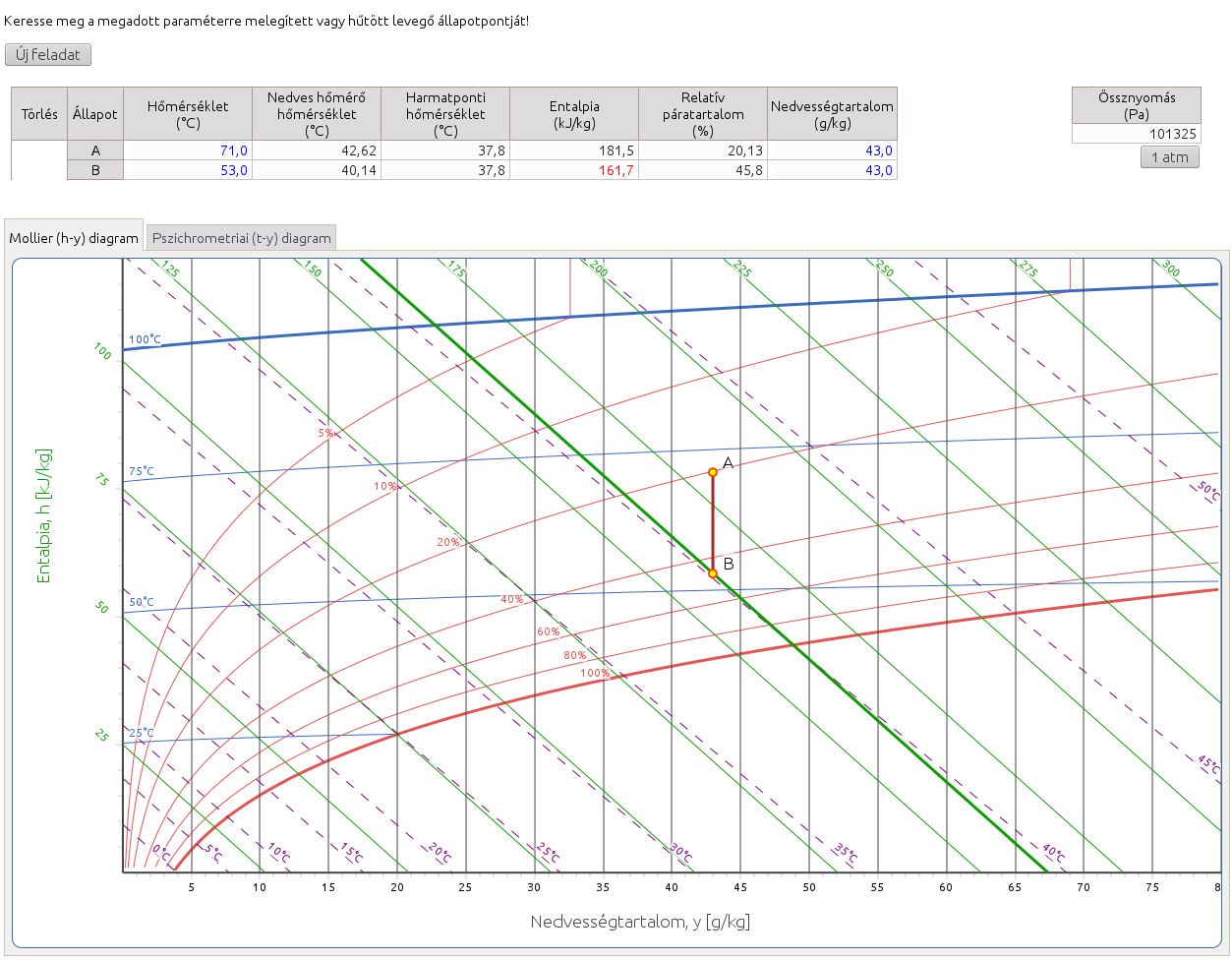
2.5. Keresse meg a megadott paraméterre melegített vagy hűtött levegő állapotpontját!
http://hyde.fastmail.jp/exercises.html#showex5
A levegőt a megadott paraméterre melegítjük, hogy adott hőmérsékletű, vagy relatív páratartalmú stb. levegőt állítsunk elő. A gőzmezőben melegítés és hűtés során az abszolút nedvességtartalom állandó marad, az állapotváltozás tehát a Mollier-féle h–y diagramon egy függőleges, a Carrier-féle pszichrometriai diagramon vízszintes egyenes mentén történik. A megoldás tehát az adott állapotponthoz tartozó állandó nedvességtartalom és a megfelelő entalpiavonal, izoterma vagy relatív páratartalom görbe metszéspontja.
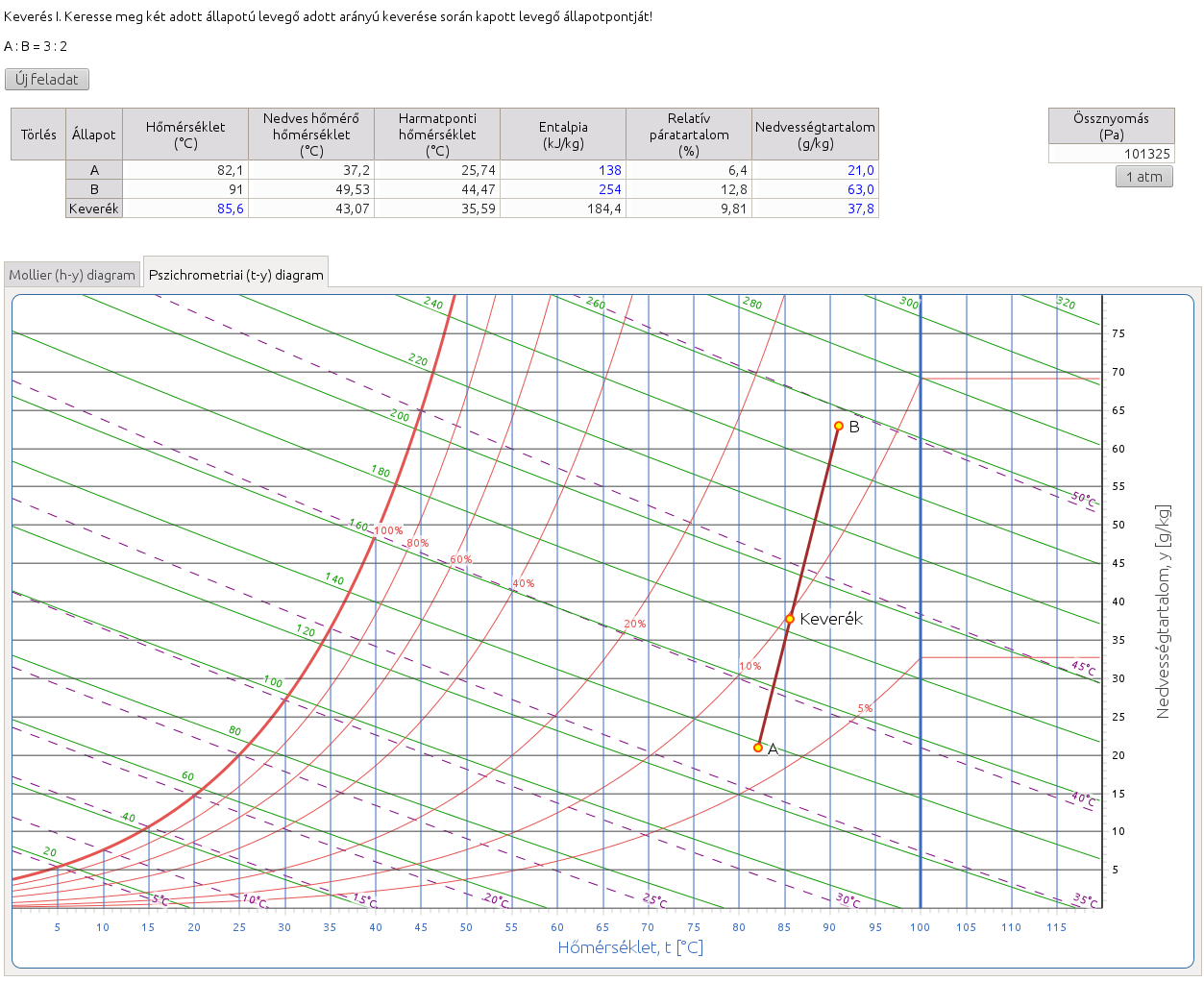
2.6. Keverés I. Keresse meg két adott állapotú levegő adott arányú keverése során kapott levegő állapotpontját.
http://hyde.fastmail.jp/exercises.html#showex6
A feladat megoldása során a megadott aránynak megfelelően a két adott állapotpont közötti szakaszt az arányokban szereplő számok összegének megfelelően felosztjuk, majd a fordított emelőszabály alkalmazásával az adott aránynak megfelelő részszakaszt a távolabbi állapotponttól felmérve kapjuk a keverék levegő állapotpontját.
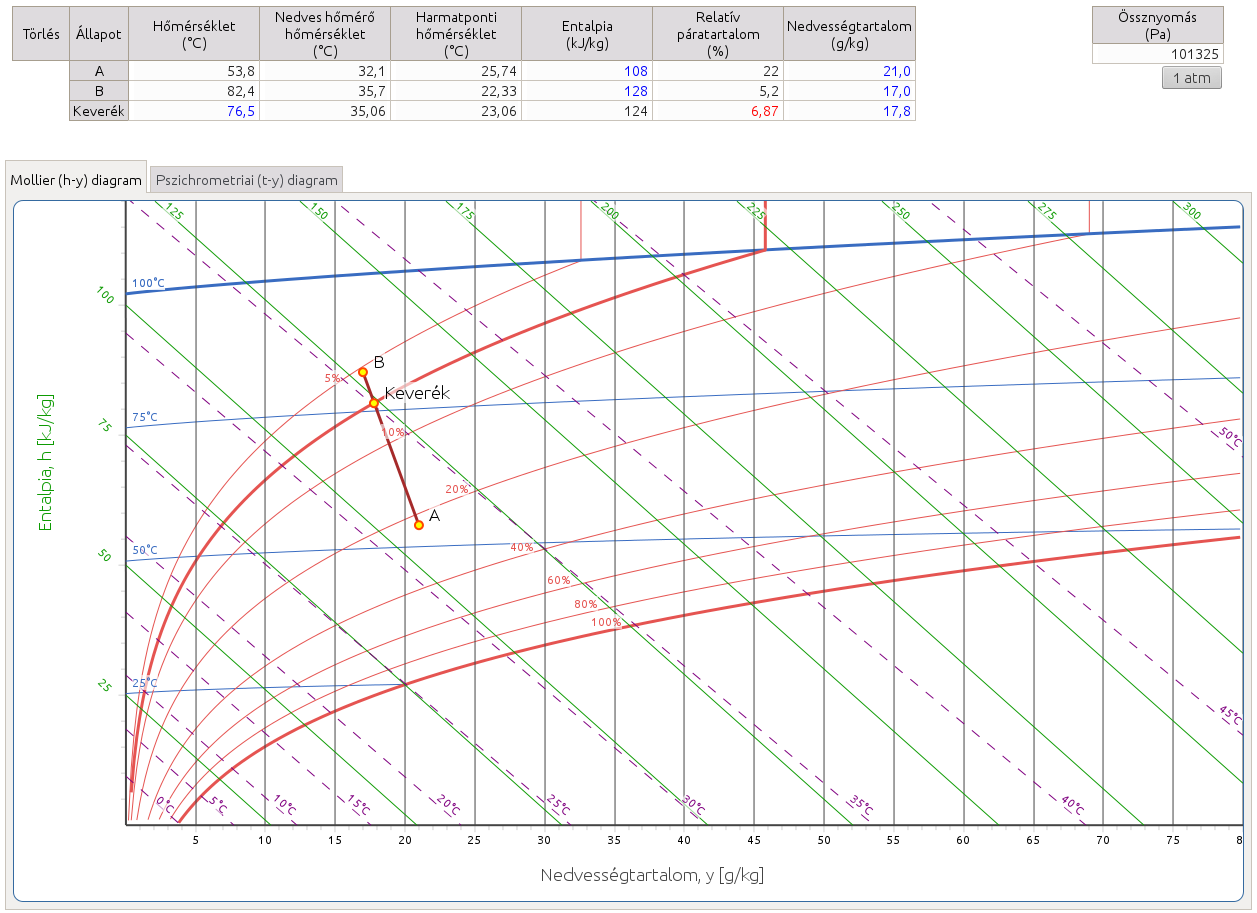
2.7. Keverés II. Keresse meg két adott állapotú levegő keverése során kapott levegő állapotpontját, ha annak egy paramétere adott!
http://hyde.fastmail.jp/exercises.html#showex7
A megoldást a Mollier-féle h–y és a Carrier-féle pszichrometriai diagramokon az adott paraméterhez tartozó görbe és az adott állapotú levegők állapotpontjai által meghatározott szakasz metszéspontja adja. Az ebben a feladatban megadott paraméterek görbéi már nem feltétlenül szerepelnek a diagramon, ezért interpolálnunk kell, lásd 2. feladathoz tartozó megjegyzéseket.
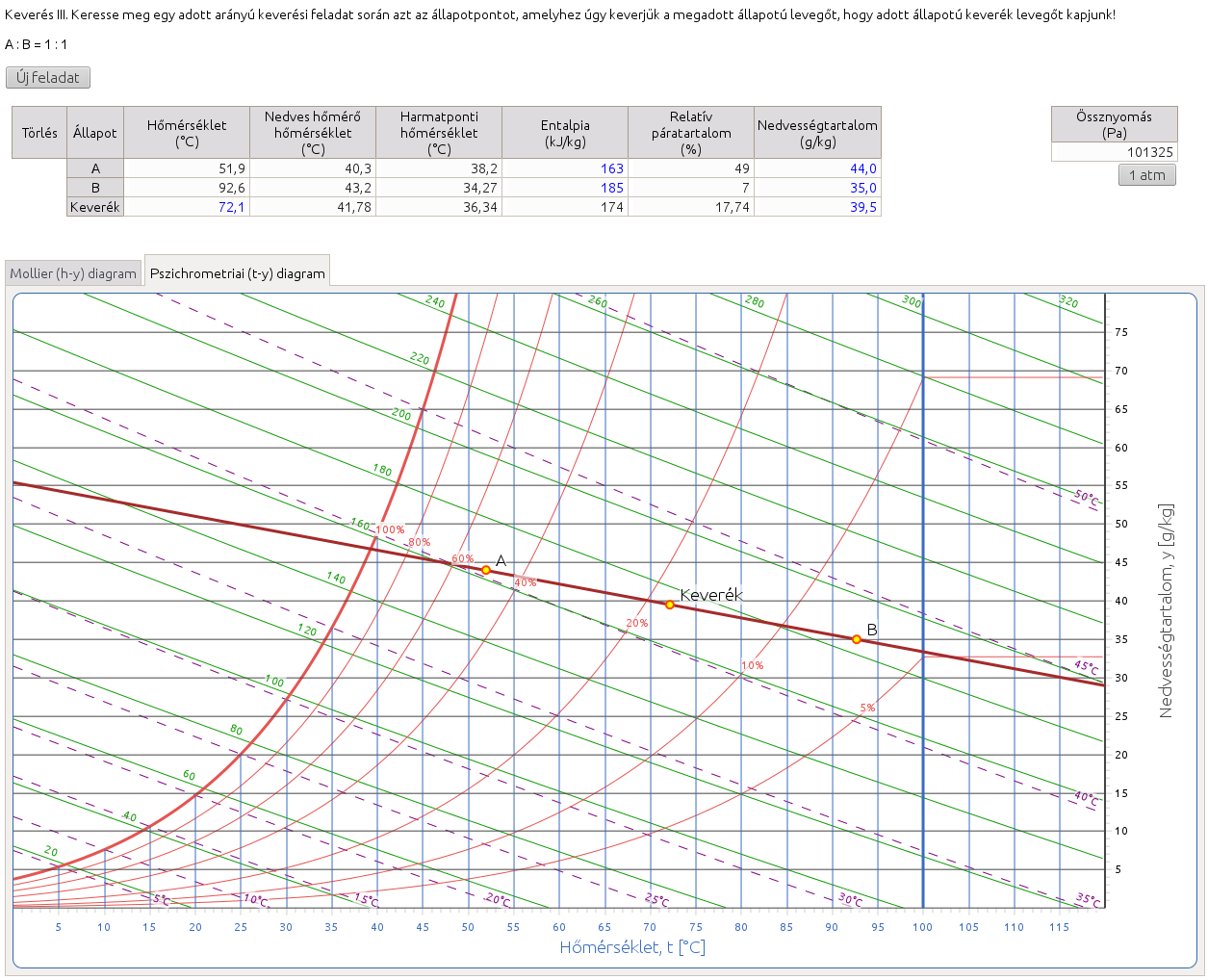
2.8. Keverés III. Keresse meg egy adott arányú keverési feladat során azt az állapotpontot, amelyhez úgy keverjük a megadott állapotú levegőt, hogy adott állapotú keverék levegőt kapjunk!
http://hyde.fastmail.jp/exercises.html#showex8
Az adott arány ismeretében, a fordított emelőszabály alkalmazásával a keverék levegő és az adott állapotú levegő állapotpontjai által meghatározott szakasz hosszát felhasználva meghatározzuk a keverék levegő és az ismeretlen állapotú levegő állapotpontjai között felmérhető szakasz hosszát és így a kérdéses állapotpontot.
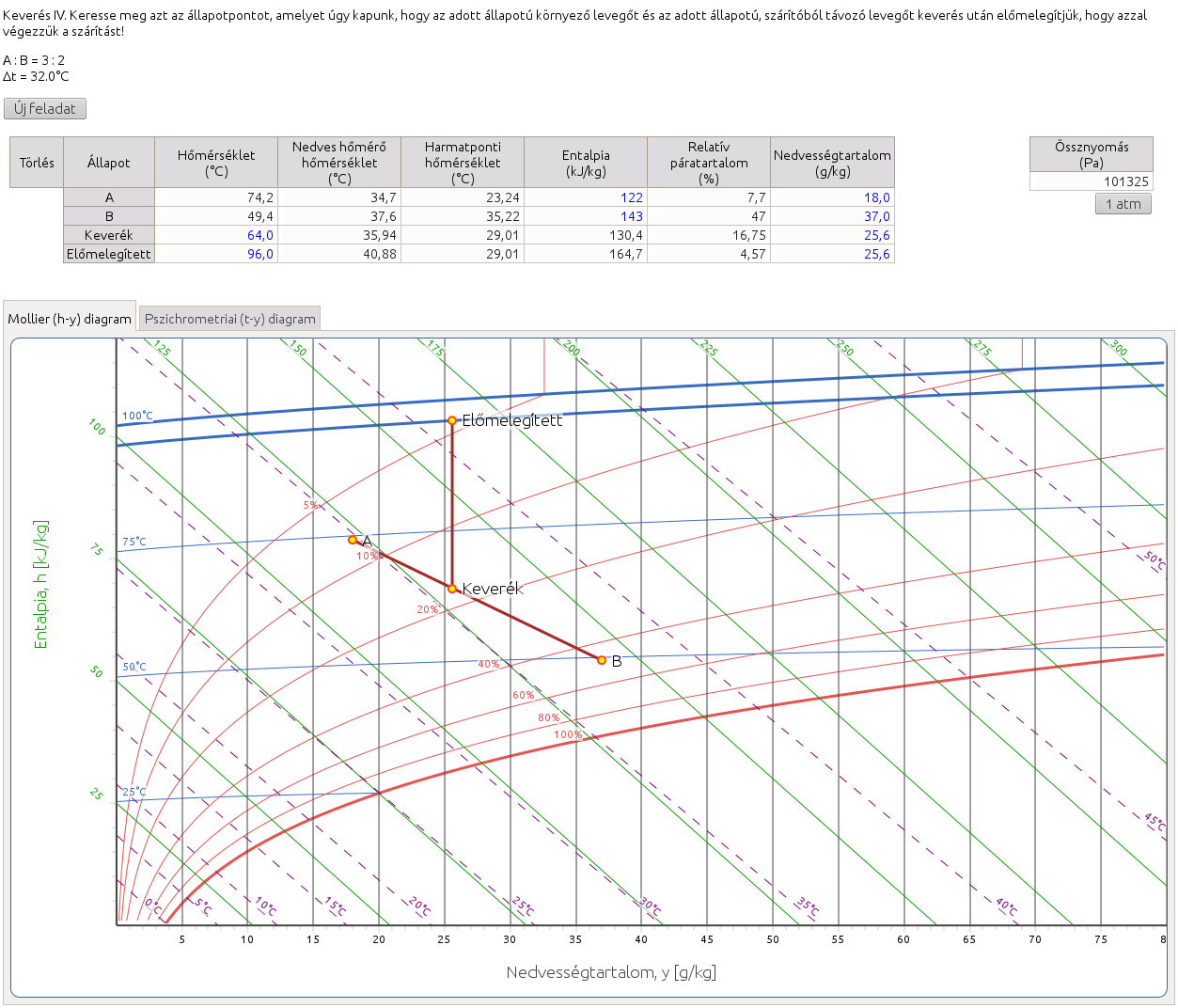
2.9. Keverés IV. Keresse meg azt az állapotpontot, amelyet úgy kapunk, hogy az adott állapotú környező levegőt és az adott állapotú, szárítóból távozó levegőt keverés után előmelegítjük, hogy azzal végezzük a szárítást!
http://hyde.fastmail.jp/exercises.html#showex9
Az adott aránynak megfelelően keressük meg a keverék levegő állapotpontját (segítségül lásd 6. feladathoz tartozó megjegyzést), majd az adott hőmérsékletváltozást figyelembe véve a kért állapotpontot (segítségül lásd 5. feladathoz tartozó megjegyzést).
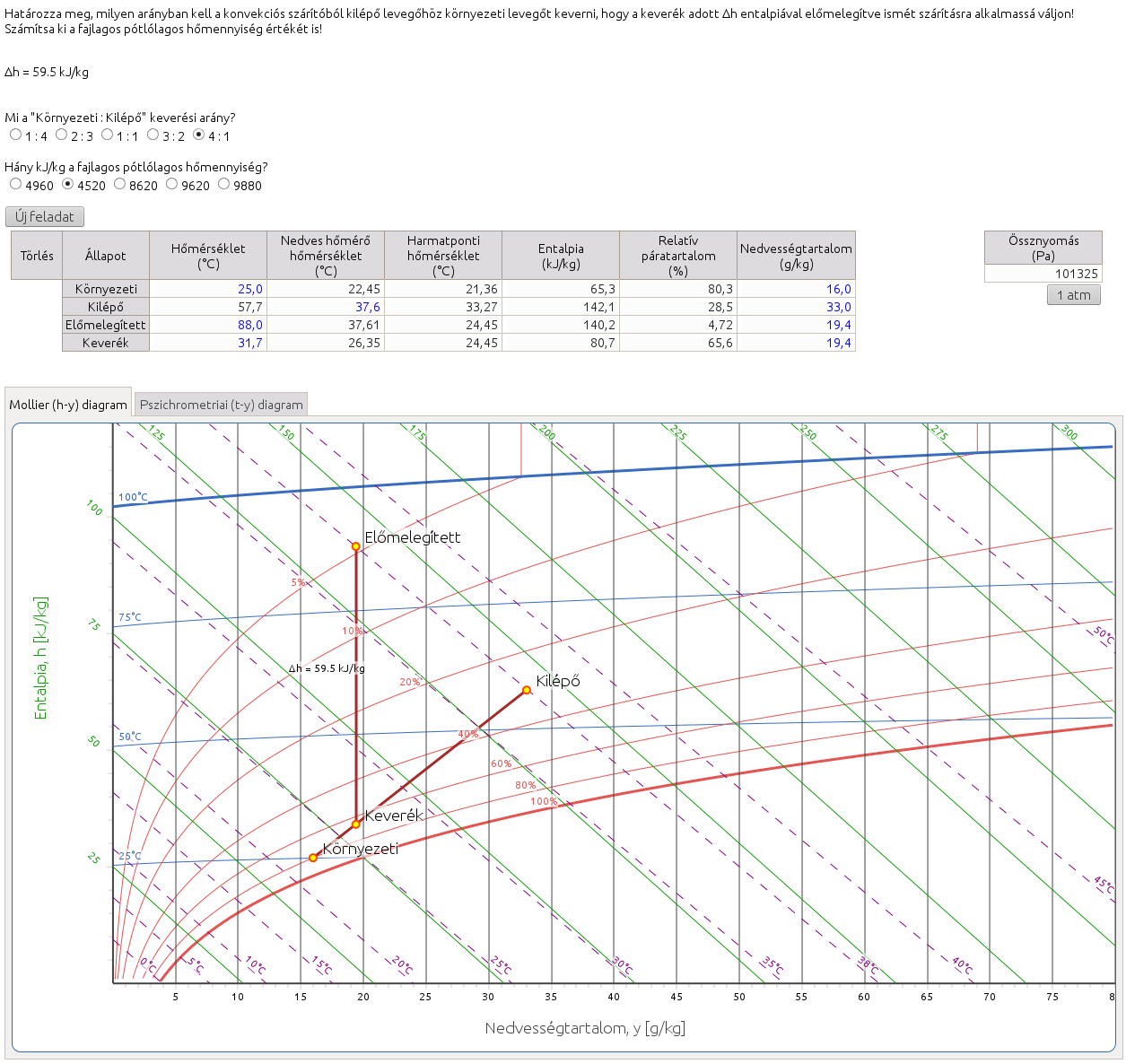
2.10. Határozza meg, milyen arányban kell a konvekciós szárítóból kilépő levegőhöz környezeti levegőt keverni, hogy a keverék adott Δh entalpiával előmelegítve ismét szárításra alkalmassá váljon! Számítsa ki a fajlagos pótlólagos hőmennyiség értékét is!
http://hyde.fastmail.jp/exercises.html#showex10
Konvekciós szárítás során előmelegített, a szárítandó anyag egyensúlyi relatív páratartalmánál (ERP) alacsonyabb páratartalmú levegőbe párolog az anyag víztartalma, továbbá ez a levegő fedezi a nedvesség elpárologtatásnak és az anyag felmelegítésének hőszükségletét is. Ha feltételezzük, hogy a folyamat hőveszteség nélkül, adiabatikusan megy végbe, akkor a szárítólevegő állapotváltozásának vonala a rajta átmenő adiabatával (ködizotermával) esik egybe. Az adiabatán a telítési görbe felé, vagyis a csökkenő hőmérséklet és növekvő nedvességtartalom irányába (a Mollier-féle diagramon jobbra lefelé, a Carrier-féle pszichrometriai diagramon balra felfelé) haladva érjük el a szárítóból kilépő levegő állapotpontját. A kilépő levegő maradék hőtartalmát hasznosíthatjuk, ha bizonyos arányban atmoszférikus levegővel keverjük, és ezt az elegyet melegítjük elő a következő szárítási művelethez. Ezt a keverési arányt kell meghatároznunk ebben a feladatban a kilépő és a környezeti levegő állapota, valamint az előmelegítéshez előírt entalpia ismeretében. Az előmelegített levegő állapotpontjának a kilépő levegő adiabatájára, a keverék állapotpontjának pedig a kilépő és a környezeti levegő állapotpontja közé kell esnie. A kettőt összekötő szakasz hosszát úgy kell beállítanunk, hogy a köztük lévő entalpiakülönbség az előírtnak megfelelő legyen. Ezután a már ismert fordított emelőszabály alkalmazásával határozhatjuk meg a kérdéses keverési arányt. A fajlagos pótlólagos hőmennyiség a
$$q+{q}_{0}=\frac{{h}_{2}-{h}_{1}}{{y}_{2}-{y}_{1}}$$
képlettel számítható, ahol:
q: az egységnyi tömegű nedvesség eltávolításához szükséges entalpiakülönbség, azaz a fajlagos pótlólagos hőmennyiség [kJ/kg]
q0: az ideális szárítástól való eltérés okozta hőveszteség (pl. nincs tökéletes szigetelés, nem adiabatikus úton megvalósuló légnedvesítés stb.), a feladatban 0-nak tekintjük [kJ/kg]
h2: a kilépő levegő entalpiája [kJ/kg]
h1: a keverék levegő entalpiája [kJ/kg]
y2: a kilépő levegő nedvességtartalma [kg/kg]
y1: az keverék levegő nedvességtartalma [kg/kg]
Figyeljünk a mértékegységekre! A táblázatban és diagramokon [g/kg]-ban feltüntetett nedvességtartalom-értékeket 1000-rel osztva válthatjuk át [kg/kg]-ba.
Irodalomjegyzék
Felhasznált irodalom:
Bara Tamásné (2008): Élelmiszerkémia (Oktatási segédanyag). Szegedi Tudományegyetem
Beke, J. (1994): Hőtechnika a mezőgazdasági és az élelmiszeripari gépészetben. Agroinform Kiadó
Bihari, P. (2001): Műszaki termodinamika. Budapesti Műszaki és Gazdaságtudományi Egyetem
Fonyó, Zs., Fábry, Gy. (1998): Vegyipari művelettani alapismeretek. Nemzeti Tankönyvkiadó
Harmatha, A. (1987): Hőtechnikai számítások személyi számítógéppel. Műszaki Könyvkiadó
Ibarz, A., Barbosa-Cánovas, G. V. (2003): Unit Operations in Food Engineering. CRC Press
Mujumdar, A. S. (2006): Handbook of Industrial Drying, Third Edition. CRC Press
Papakonstantinou, J. (2007): The Historical Development of the Secant Method in 1-D. Mathematical Association of America
Singh, R. P., Heldman, D. R. (2009): Introduction to Food Engineering, Fourth Edition. Academic Press
Todorovic, B. (2007): Visualization of air conditioning and ventilation processes: the appearance of humid air diagram within a short period at three distant places on a globe. 2nd PALENC Conference and 28th AIVC Conference on Building Low Energy Cooling and Advanced Ventilation Technologies in the 21st Century, Greece
Verhás, J. (ed.) (1998): Élelmiszeripari termodinamika. Kertészeti és Élelmiszeripari Egyetem
Ajánlott irodalom:
Brennan, J. G. (1997): Food Dehydration – A Dictionary and Guide, CRC Press
Yanniotis, S. (2008): Solving Problems in Food Engineering, Springer